2014-02-02
435
Определение. Точкой разрыва функции называется внутренняя точка области задания функции, в которой нарушается непрерывность функции.
Если в точке разрыва функция, к тому же, не существует, ее часто называют особой точкой. Так функция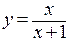 
существует на всей числовой оси, кроме точки 
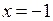. Эта точка – особая, и в ней функция терпит разрыв.
Разрыв может быть конечным, есл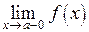и 
и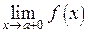 
принимают конечные, но не равные значения. Разность между этими значениями называют скачком функции в точке разрыва.
Пример. Функция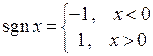 
. Очевидно, 
,
.
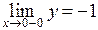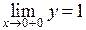Разрыв бесконечный, если левый, правый или оба предела бесконечны.
Пример.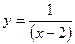 
. Имеем 
, 
.
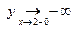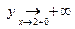Разрыв называется устранимым, если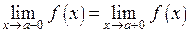 
и эти пределы конечны, но функция в точке 
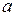не задана.
Пример. Функция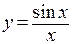 
не может быть задана при 
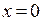(деление на ноль), однако и левый и правый ее пределы равны 1, что следует из первого замечательного предела.
Устранить этот недостаток можно введением другой функции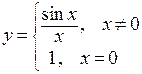 
. Эта функция совпадает с заданной во всех точках, кроме 0, но она существует и непрерывна на всей числовой оси, что следует из свойств непрерывной функции.
