Вычисление пределов. Вначале выясним, в чем смысл вычисления пределов?

Вначале выясним, в чем смысл вычисления пределов? В точках, где функция 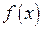определена и непрерывна, соответствующий предел можно получить, вычислив ее значение. Особый подход к вычислению предела необходим, когда желательно знать поведение функции в окрестности особой точки, или установить, как ведет себя функция при стремлении ее аргумента к бесконечности.

Рассмотрим функци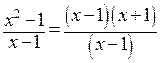и и 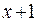.Последняя получена в результате формального сокращения числителя и знаменателя первой на множитель 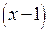. Это разные функции, так как имеют разные области существования, хотя их значения совпадают повсюду, кроме точки 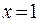. В этой точке первая функция не существует (деление на ноль), вторая равна 2. Теперь вычислим предел 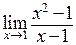. Рассмотрим последовательность действий 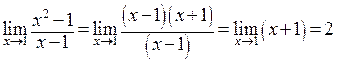под знаком предела. Здесь мы заменяем одну функцию на другую в той области, где они совпадают, ибо при вычислении предела 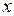стремится к предельной точке 1, не попадая в саму эту точку. Итак, рассматриваемая функция в точке 1 не существует, но стремится к значению 2 при .

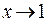Исследуем 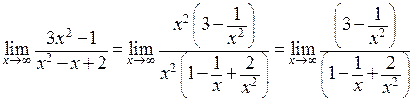. Он равен 3, так как 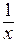и 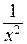являются бесконечно малыми при 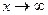. Сокращение на 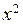также законно, поскольку 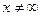, а только стремится к ней, то есть принимает сколь угодно большие, но конечные значения.