Непрерывность функции. Определение 1. Функция непрерывна в точке , если предел этой функции при равен значению функции в предельной точке

Определение 1. Функция 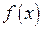непрерывна в точке 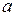, если предел этой функции при 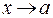равен значению функции в предельной точке, то есть .

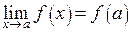Применяя второе определение предела функции в точке, получим

Определение 2. Функция 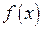непрерывна в точке 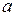, если .

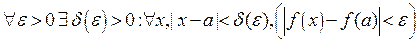Определение 3. Функция 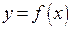непрерывна в точке 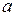, если 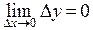, где 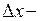приращение аргумента функции (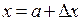), а 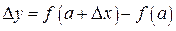– приращение функции, соответствующее приращению ее аргумента .

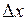Доказательство следует из первого определения непрерывной функции

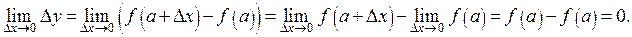Здесь первый из пределов вычисляется с помощью определения 1, второй – как предел постоянной, поскольку 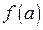не зависит от .

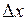Определение 4. Функция 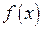непрерывна в точке 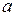, если

.

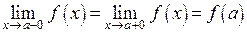Определение 5. Функция 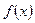непрерывна в некоторой области, если она непрерывна во всех точках этой области.