Все степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции непрерывны в областях существования.
1) Сумма непрерывных функций – есть непрерывная функция.
Действительно, из определения 1 непрерывности следует, что если 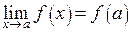 и
и 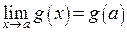 , то
, то
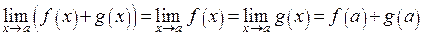 .
.
2). Произведение непрерывных функций есть функция непрерывная.
3). Частное непрерывных функций – функция непрерывная, если знаменатель в предельной точке не равен нулю.
Доказательства второго и третьего свойств также следует из свойств пределов.
4). Пусть функция 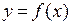 непрерывна в точке
непрерывна в точке 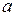 , пусть функция
, пусть функция 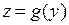 непрерывна в точке
непрерывна в точке 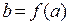 . Тогда функция
. Тогда функция  непрерывна в точке
непрерывна в точке 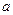 .
.
Очевидно, что 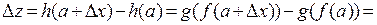
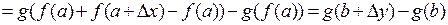 .
.
Так как согласно определению 3 непрерывности 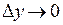 при
при 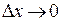 и
и 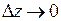 при
при 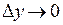 , получим:
, получим: 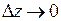 при
при 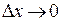 .
.
Таким образом, непрерывная функция от непрерывной функции есть функция непрерывная.
Пример. Функция  непрерывна во всех точках числовой оси, так как функция
непрерывна во всех точках числовой оси, так как функция 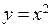 непрерывна на
непрерывна на 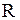 , а функция
, а функция 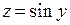 непрерывна на множестве неотрицательных чисел.
непрерывна на множестве неотрицательных чисел.
 2014-02-02
2014-02-02 360
360








