2014-02-02
693
Градиент.
Для обозначения градиента функции используется символ grad u:
Grad u:{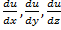
}
Аналогично в случае функции двух переменных
Z= f(x,y) имеем:
Grad z:{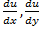
}
Пример: Найти: градиент и его модуль функции z=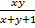 
в точке М(0,1)
Решение: По формуле имеем для функции двух переменных Grad z: {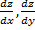
}= {
}
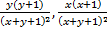При х=0 и y= 1 получаем:
Grad z|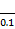
= {1, 0}, |Grad z|=1
Частные производные и дифференциалы высших порядков.
Частными производными 2-ого порядка от функции z=f (x,y) называется частные производные от её частных производных 1-го порядка:
;
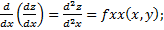
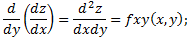
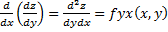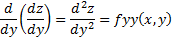
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они не прерывны.
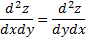
Пример:
Z= y lnx
Найти: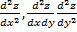 
Решение: найдем частное производное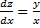 
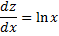
Дифференцируя повторно получаем:
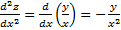
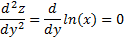
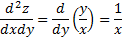
Экстремум функции 2-х независимых переменных.
Экстремум функции. Функция z=f (x,y) имеет максимум (минимум) в точке М0 (x0,y0) если значения функции в этой точке больше (меньше), чем её значение в любой другой точке М (x,y) некоторой окрестности точки М0, т.е. f (x0,y0)> f (x,y) соответственно f (x0,y0) < f (x,y) для всех точек М(x,y) удовлетворяющих условию | М0 М |< δ, где δ достаточно малое положительно число. Максимум или минимум функции называется экстремумом. Точка М0, в которой функция имеет экстремум, называется точкой экстремума. Если дифференцируемая функция z=f (x,y) достигая экстремума в точке М0 (x0,y0) то её частные производные 1-го порядка в этой точке равны 0, т.е.
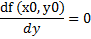
Точки, в которых частные производные равны 0 называются стационарными точками. Не всякая стационарная точка является точкой экстремума. Пусть М0 (x0,y0) стационарная точка функции z=f (x,y).
Обозначаем: А=
; В= 
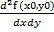, C=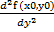
Составим дискриминант. ∆= АС-В²,
