Пример №1
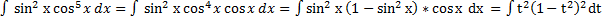 , где t= sin x
, где t= sin x
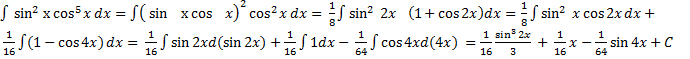 /
/
Интегралы, содержащие иррациональность.
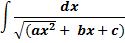
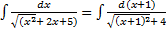 = ln |x+1+
= ln |x+1+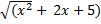 | +C
| +C
Выделяется полный квадрат
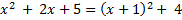
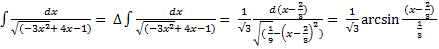 + C=
+ C=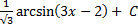
Интегралы вида:
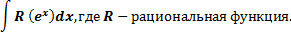
С помощью подстановки 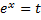 , откуда
, откуда 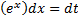
Dx= 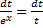
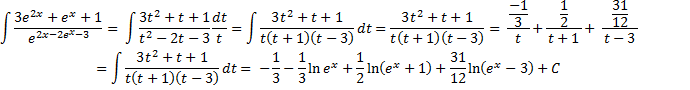

D=4-3=1
X1= 3
X2= -1
Определенный интеграл.
Если функция f(x) определена на отрезке a≤x≤b b a=x0≤ x1 ≤ x0≤ …≤ xn-1≤ xn=b -произвольное разбитие этого отрезка на n частей, то интегральной суммой функции f(x) на отрезке [a,b] называется сумма вида:
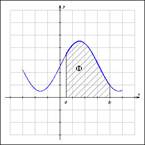
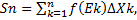
Где Xk-1 ≤ Еk ≤ Xk
∆Xk= Xk - Xk-1, k= 1,2,3…n- основания прямоугольников.
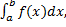 т.о.
т.о.
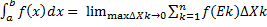
f(Еk)- высоты прямоугольников.
Свойства определенных интегралов.
1. При перестановке пределов интегрирования знак интеграла меняется на противоположный.
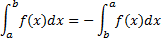
2. Постоянный множитель можно вынести за знак определенного интеграла.
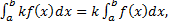 где k- постоянная величина.
где k- постоянная величина.
3. Определенный интеграл от алгебраической суммы функции равен алгебраической сумме определенных интегралов от этих функций.
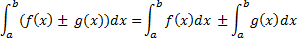
4. Если a, b, c принадлежат интервалу, на котором функция 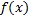 непрерывна, то
непрерывна, то
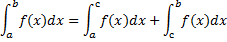
5. Если функция 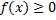 всюду на отрезке [a,b], то
всюду на отрезке [a,b], то
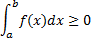
6. Если на отрезке 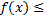 g(x) всюду на отрезке [a,b], то
g(x) всюду на отрезке [a,b], то
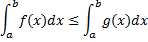
7. Если функция 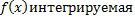 на отрезке [a,b], то
на отрезке [a,b], то
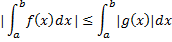
8. 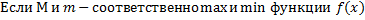 на отрезке [a,b], то
на отрезке [a,b], то
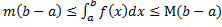
9. Теорема о среднем. Если g(x)=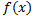 непрерывна на отрезке [a,b], то найдется такое значение Е e [a,b], что
непрерывна на отрезке [a,b], то найдется такое значение Е e [a,b], что
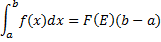
10. Если функция 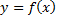 четная, то
четная, то
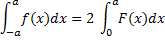
Если функция  нечетная, то
нечетная, то
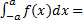 0
0
11. Формула Ньютона- Лейбница. Определенный интеграл от непрерывной на отрезке [a,b] функции 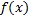 равен приращению любой ее первообразной F(x) на этом отрезке:
равен приращению любой ее первообразной F(x) на этом отрезке:
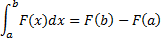
Или
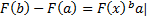
12. Замена переменной в определенном интеграле. Если функция φ(t) имеет непрерывную производную на отрезке [α, β], a= φ(α) и b= φ (β) и функция 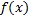 непрерывна в каждой точке х= φ(t), где t e[α, β], то
непрерывна в каждой точке х= φ(t), где t e[α, β], то
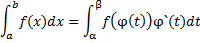
13. Интегрирование по частям определенного интеграла. Если функция u=u(x), v=v(x) имеют производные на отрезке [a,b], то
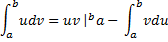
 2014-02-02
2014-02-02 408
408








