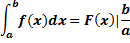
Пример:
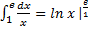 = ln e- ln1=1-0=1
= ln e- ln1=1-0=1
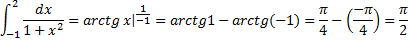
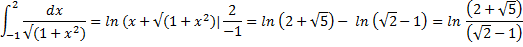
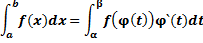
Пример:
t=1+x² dt=2x dt, t=1
при х=0 и t=2, при х=1
т.к. х=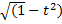 непрерывна [1.2] то и новая подынтегральная функция также непрерывна => для нее существует первообразная на этом отрезке, получаем:
непрерывна [1.2] то и новая подынтегральная функция также непрерывна => для нее существует первообразная на этом отрезке, получаем:
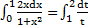 = ln t|
= ln t| 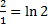
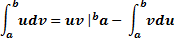 Пример:
Пример:
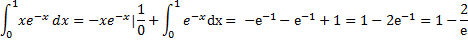
u=x, du= dx
dv=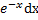 , v=
, v= 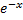

Площадь плоской фигуры:
Площадь криволинейной трапеции равна определенному интегралу от функции f(x)на отрезке [a,b] S= 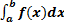
Пример:
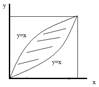
Найти S фигуры ограниченной линиями y=√x, y=x³.
Решение: вычислим абсциссы точек пересечения указанных кривых для чего приравняем правые части этих уравнений. √ x=x³.
Корни этого уравнения х1=0, х2=1.=> 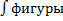 , ограниченной сверху y=√x и y=x³ дается определение
, ограниченной сверху y=√x и y=x³ дается определение 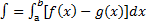 на отрезке [0,1]
на отрезке [0,1]

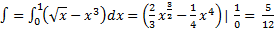
Пример:
Найти площадь фигуры, ограниченной графиком функции y=ln x≥0, осью Ох и прямой х=2
Решение: отрезок интегрирования 1≤х≤2, так что искомая площадь согласно формуле равна
S=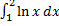 = x ln x |
= x ln x | -
- 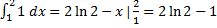
Объем тел вращения:
 Вокруг оси Ох:
Вокруг оси Ох: 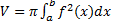 Вокруг оси Оy:
Вокруг оси Оy: 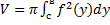
Пример:
Кривые y=x², y=√x [0,1]
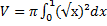 -
-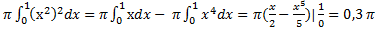
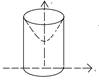 Кривые y=ex, x=0,x=1,y=0
Кривые y=ex, x=0,x=1,y=0
Выражаем x=lny 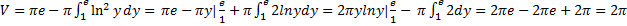
 2014-02-02
2014-02-02 338
338








