2014-02-02
350
Рассмотрим степенной ряд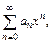 
(*)
имеющий радиус сходимости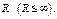 
Сумма ряда 
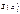есть ф-я определенная внутри интервала сходимости, а также на тех концах интервала, где ряд сходится.
Лемма 1. Степ-й ряд равномерно сходится в любом интервале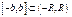 
Док-во. Выберем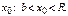 
По теореме Абеля ряд 
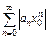сходится. 
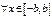имеем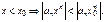 
Последнее рав-во означает, что ряд (*) равномерно сходится в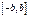 
Лемма 2. Степ-й ряд, составл-й из производных ряда (*) имеет тот же радиус сход-ти, что и ряд (*).
Док-во. Допустим, что сущ-ет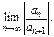 
Тогда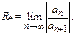 
Ряд производных имеет вид 
(**)
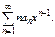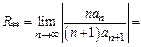
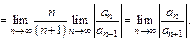
Если составить ряд из производных ряда (**), то у него тоже радиус сходимости равен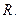 
Т. е. все степ-е ряды, полученные последовательным диф-нием ряда (*) имеют одинаковый радиус сходимости и равномерно сходятся в любом интервале, принадлежащим области сходимости.
Св-ва. 1) Сумма степ-го ряда есть ф-я, непрерывная в интервале сходимости ряда.
Пример.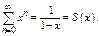 
Ф-я 
непрерывна всюду, за исключением точки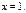 
Но она явл-ся суммой ряда только при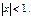 
2) Степ-й ряд можно почленно интегрировать в интервале сходимости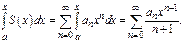 
3) Степ-й ряд можно почленно диф-ть любое число раз в интервале сходимости.
