Определение. Степенным рядом наз-т функц-й ряд 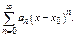 (*) Если
(*) Если 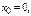 то имеем ряд
то имеем ряд 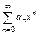 (**)
(**)
В дальнейшем будем рассматривать ряды вида (**), т. к. они сводятся к рядам вида (*) подстановкой 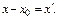
Теорема Абеля. Если степенной ряд (**) сходится в точке  то он сходится абсолютно в интервале
то он сходится абсолютно в интервале 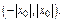
Док-во. Т. к. ряд 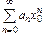 сходится, то
сходится, то 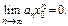 Тогда
Тогда 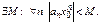 Запишем (**) так:
Запишем (**) так: 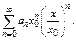 Ряд из абсолютных величин сходится
Ряд из абсолютных величин сходится 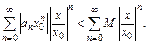 т. к.
т. к. 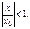 Значит ряд (**) сходится абсолютно.
Значит ряд (**) сходится абсолютно.
Следствие. Если ряд (**) расходится при 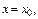 то он расходится
то он расходится 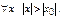
Обл-ть сходимости. Возможны три случая:
1) Обл-ть сходимости состоит только из одной точки 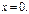
Пример. 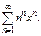 Действ-но
Действ-но 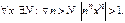
2) Обл-ть сходимости 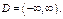
Пример. 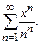 Действ-но
Действ-но 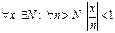 и для
и для 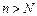 члены ряда меньше сходящейся геом-й прогрессии.
члены ряда меньше сходящейся геом-й прогрессии.
3) Область 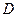 ограничена.
ограничена.
Пример. 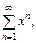

Определение. Радиусом сходимости степ-го ряда (**) наз-ся такое число 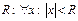 ряд сходится,
ряд сходится, 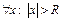 - расходится.
- расходится.
Интервал 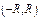 наз-ся интервалом сходимости.
наз-ся интервалом сходимости.
В первом примере 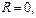 во втором -
во втором - 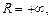 в третьем -
в третьем - 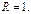
Для определения радиуса сходимости нужно исследовать ряд. Рассмотрим ряд 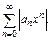 Применим признак д’Аламбера
Применим признак д’Аламбера 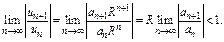 Тогда
Тогда 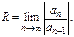 Если
Если 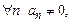 то применяя радикальный признак Коши получим
то применяя радикальный признак Коши получим 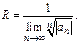
Рассмотрим ряд 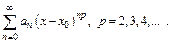 Применяя признак д’Аламбера, получим
Применяя признак д’Аламбера, получим 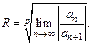
Рассмотрим ряд 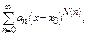 где
где 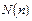 произв-ая ф-я аргумента
произв-ая ф-я аргумента 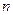 . Для определения обл-и сходимости применяют признак д’Аламбера.
. Для определения обл-и сходимости применяют признак д’Аламбера.
Пример 1. 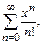
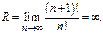
Пример 2. 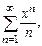
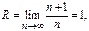
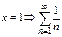 - ряд расходится,
- ряд расходится, 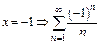 - ряд сходится условно. Окончательно
- ряд сходится условно. Окончательно 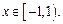
Пример 3. 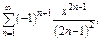
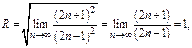
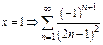 - ряд сходится,
- ряд сходится, 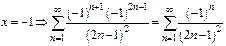 - ряд сходится,
- ряд сходится, 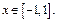
Пример 4. 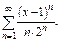
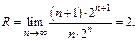
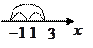
 - ряд сходится условно,
- ряд сходится условно, 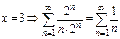 - ряд расходится,
- ряд расходится, 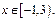
 2014-02-02
2014-02-02 469
469








