Запишем ф-ю 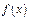 в виде
в виде 
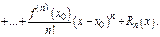
Докажем теорему о структуре 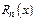 , которая позволит устанавливать, стремится ли
, которая позволит устанавливать, стремится ли 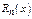 к нулю при
к нулю при 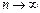 , т. е. разлагается
, т. е. разлагается 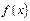 в ряд Тейлора или нет.
в ряд Тейлора или нет.
Теорема. Если 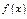 во всех точках некоторого интервала, содержащего точку
во всех точках некоторого интервала, содержащего точку 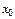 , имеет производную
, имеет производную 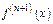 , то для всякой точки, принадлежащей интервалу, остаточный член равен
, то для всякой точки, принадлежащей интервалу, остаточный член равен 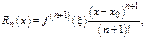 где
где 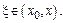
Док-во. Запишем остаточный член в виде
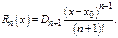 Найдем
Найдем  такое, чтобы для всякого
такое, чтобы для всякого 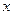 , принадлежащего интервалу, выполнялось
, принадлежащего интервалу, выполнялось 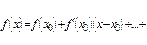
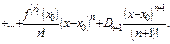
Зафиксируем 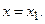 Тогда
Тогда  Докажем, что это выражение равно
Докажем, что это выражение равно 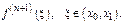
При 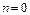 из теоремы Лагранжа
из теоремы Лагранжа 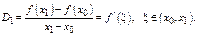
Для других 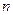 построим вспомогательную ф-ю
построим вспомогательную ф-ю 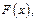 удовлетворяющую теореме Роля. Пусть
удовлетворяющую теореме Роля. Пусть 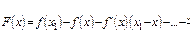
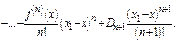
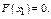 При
При 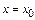 заменив
заменив 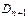 его значением, получим
его значением, получим 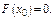 Найдем
Найдем 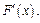
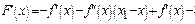

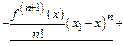
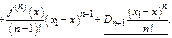 Только подчеркнутые члены не сокращаются. Производная
Только подчеркнутые члены не сокращаются. Производная 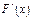 сущ-ет во всех точках интервала. Вынося общий множитель за скобки, получим
сущ-ет во всех точках интервала. Вынося общий множитель за скобки, получим 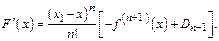 Подставим вместо
Подставим вместо 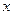 значение
значение 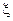 при котором
при котором 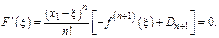 Тогда
Тогда 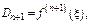 т. е.
т. е. 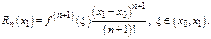 Т. к.
Т. к. 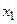 - любая точка интервала, то теорема доказана.
- любая точка интервала, то теорема доказана.
Формула Тейлора для ф-и 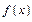 в точке
в точке 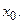
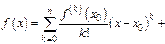
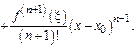
При выводе формулы предполагалось, что 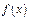 имеет производные до
имеет производные до 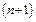 -й, где
-й, где 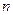 какое-то число. Другие производные нас не интересовали.
какое-то число. Другие производные нас не интересовали.
Частные случаи
1) 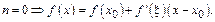 Это формула Лагранжа.
Это формула Лагранжа.
2) 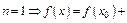
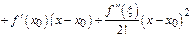 или
или 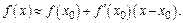 Это линейная аппроксимация.
Это линейная аппроксимация.
Т. к. 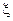 - неизвестна, то
- неизвестна, то 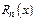 нужно только оценить. Пусть в интервале, где формула Тейлора справедлива,
нужно только оценить. Пусть в интервале, где формула Тейлора справедлива, 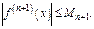 Тогда для всякого
Тогда для всякого 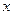 принадлежащего интервалу
принадлежащего интервалу 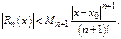
Док-во. 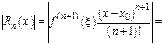
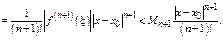
 2014-02-02
2014-02-02 415
415








