Одним из ключевых показателей, используемых при оценке целесообразности инвестиций в тот или иной вид актива, является доходность финансового актива. В общем случае это относительный показатель, рассчитываемый как отношение абсолютной величины дохода, генерируемого данным активом, и величины инвестиции в этот актив.
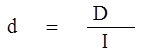 (6.3)
(6.3)
где D – абсолютная величина дохода по активу;
I – величина инвестиции в актив.
В зависимости от вида финансового актива в качестве дохода D чаще всего выступают дивиденд, процент, прирост капитализированной стоимости. Таким образом, существуют различные варианты расчета доходности. Этот показатель измеряется в процентах или долях единицы.
В анализе речь может идти о двух видах доходности – фактической и ожидаемой. Первая рассчитывается post factum и имеет значение лишь для ретроспективного анализа. Гораздо больший интерес представляет ожидаемая доходность, которая рассчитывается на обнове прогнозных данных в рамках имитационного перспективного анализа и используется для принятия решения о целесообразности приобретения тех или иных финансовых активов. Логика расчета показателей доходности может быть описана следующим образом.
Приобретая некий финансовый актив, например акции, инвестор вправе рассчитывать на два вида потенциальных доходов: а) дивиденд; б) доход от прироста капитала. Очевидно, что оба поступления не являются безусловньми и могут состояться, как правило, в случае эффективной работы компании, чьи акции приобретены. Оговорка «как правило» сделана потому, что, например, динамика дивидендов и прибыли совершенно не обязаны совпадать. Так, многие компании в экономически развитых странах нередко считают целесообразным выплатить дивиденды даже в том случае, если отчетный год закончен с убытком. Причина такой на первый взгляд нелогичной политики заключается в том, чтобы избежать нежелательных последствий сигнального эффекта негативной информации.
В отношении доходности считается, что цена финансового актива, приобретенного (или возможного к приобретению по желанию инвестора) в некоторый момент времени t0, когда и проводится анализ, определенно известна и равна Р0. Известен и регулярный доход D0 в виде процентов или дивидендов, полученных за период, истекший в момент времени t0. Ожидается, что за следующий период t1 регулярный доход составит величину D1 и по истечении данного периода актив может быть реализован по цене P1 (ожидаемая величина). Величина (P1 – Р0) представляет собой доход от прироста капитала (или доход от капитализации).
Итак, в данной схеме в отношении D0 и Р0 известны их фактические значения, D1 представляет собой исходную прогнозную оценку, а Р1 является целевым расчетньм показателем. Обычно считается, что Р1 > Р0, хотя в принципе выполнение этого неравенства не является обязательным, и в этом случае говорят об убытке от капитализации и соответствующей ему отрицательной доходности.
Таким образом, общий доход, генерируемый инвестицией Р0, за данный период t1 составит величину D1 + (P1 – P0), а общая доходность d будет равна:
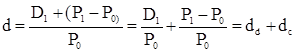 (6.4)
(6.4)
Первое слагаемое dd в формуле (4) представляет собой текущую доходность (в приложении к акциям она называется также дивидендной), второе слагаемое dc носит название капитализированная доходность. Из приведенной формулы хорошо видно, что общий доход (или, что в данном случае равносильно, общая доходность) имеет два компонента, причем в зависимости от успешности работы и стратегии развития компании, эмитировавшей данный актив, весомость того или иного компонента может быть различной. Таким образом, выбирая для покупки акции той или иной компании, инвестор должен расставить для себя приоритеты – что важнее, дивиденды или доход от прироста капитала.
Формула (4) дает простейший алгоритм расчета доходности, однако возможен и другой подход в рамках фундаменталистской теории. Логика рассуждений в этом случае такова.
Если предположить, что рынок ценных бумаг является эффективным и находится в состоянии равновесия, то в отношении конкретного финансового актива в любой момент времени известны его текущая цена и доходы, которые, как ожидается, этот актив будет генерировать в будущем. Зная эти оценки, можно вычислить параметр r формулы (1), полученное значение которого и можно трактовать как общую доходность данного актива.
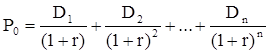 (6.5)
(6.5)
Значение Р0 представляет собой оценку текущей внутренней стоимости финансового актива и в условиях эффективного и равновесного рынка совпадает с его текущей рыночной ценой на начало периода t0. Если делать оценку актива с позиции конца периода t1, то исходный поток ожидаемых поступлений связан с текущей ценой актива следующей формулой:
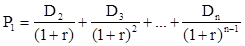 (6.6)
(6.6)
Таким образом, формула (5) преобразуется следующим образом:
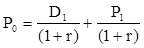 (6.7)
(6.7)
Отметим, что смысл знаменателя второго слагаемого в формуле (7) заключается в дисконтировании P1, т.е. приведении ее к моменту времени t0. Разрешая это уравнение относительно r, и обозначая его через d, как раз и получим формулу (4).
Следует обратить внимание, что в зависимости от вида финансового актива и абсолютных показателей, выбранных для его характеристики, можно исчислить несколько числовых характеристик доходности. Поскольку их значения могут существенно различаться, нельзя говорить о некой абстрактной доходности, необходимо обязательно уточнять, о чем идет речь, какой алгоритм используется для расчета. В данной лекции мы не будем рассматривать формулы расчета для конкретных финансовых инструментов, поскольку это было сделано в более ранних курсах.
 2014-02-02
2014-02-02 1524
1524
