Модель оценки доходности финансовых активов

Любая организация может рассматриваться как совокупность некоторых активов, находящихся в определенном сочетании. Владение любым из этих активов связано с определенным риском в плане воздействия на этого актива на величину общего дохода организации.

Это утверждение вполне уместно и для портфеля ценных бумаг, которыми обладает коммерческий банк. Очевидно, что степень риска изменяется обратно пропорционально количеству включенных в портфель случайным образом видов ценных бумаг (Рисунок 6.1). А общий риск портфеля состоит из двух частей:

· диверсифицируемый (несистематический) риск, т.е. риск, который может быть элиминирован за счет диверсификации (инвестиро­вание 1 млн. руб. в акции десяти компаний менее рискованно, нежели инвестирование той же суммы в акции одной компании);

· недиверсифицируемый (систематический, или рыночный) риск, т.е. риск, который нельзя уменьшить путем изменения структуры портфеля.

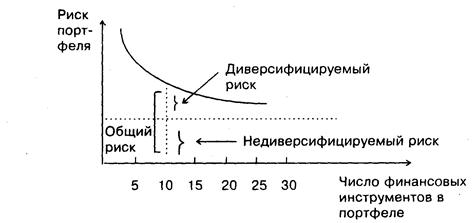
Рис. 6.1. Зависимость степени риска от диверсификации портфеля

Исследования показали, что если портфель состоит из 10–20 различных видов ценных бумаг, включенных в портфель с помощью случайной выборки из имеющегося на рынке ценных бумаг набора, то несистематический риск может быть сведен к минимуму (это по­казано и на рис. 1). Таким образом, этот риск поддается элимини­рованию довольно несложными методами, поэтому основное вни­мание следует уделять возможному уменьшению систематического риска.

В экономической теории существует «теория портфеля» (portfolio theory) – теория финансовых инвестиций, в рамках которой с помо­щью статистических методов и осуществляются наиболее выгодное распределение риска портфеля ценных бумаг и оценка прибыли. Эта теория состоит из четырех основных элементов:

· оценка активов (security valuation);

· инвестиционные решения (asset allocation decision);

· оптимизация портфеля (portfolio optimization);

· оценка результатов (performance measurement).

В процессе управления инвестиционным портфелем менеджер постоянно сталкивается с задачей отбора новых инструментов и ана­лиза возможности их включения в портфель. Какими же методами можно это делать? Существует несколько способов, однако наибольшую известность получила модель оценки доходности финансовых активов (Capital Asset Pricing Model, САРМ), увязывающая систематический риск и доходность портфеля.

Как и любая теория финансов, модель CAPM сопровождается рядом предпосылок, которые в акцентированном виде были сформули­рованы М. Дженсеном и опубликованы им в 1972 г. [Jensen, 1972]. Эти предпосылки таковы.

1.Основной целью каждого инвестора является максимизация возможного прироста своего богатства на конец планируемого периода путем оценки ожидаемых доходностей и среднеквадратических отклонений альтернативных инвестиционных портфелей.

2.Все инвесторы могут брать и давать ссуды неограниченного размера по некоторой безрисковой процентной ставке d_rf, при этом не существует ограничений на «короткие» продажи любых активов[1].

3.Все инвесторы одинаково оценивают величину ожидаемых зна­чений доходности, дисперсии и ковариации всех активов; это означа­ет, что инвесторы находятся в равных условиях в отношении прогно­зирования показателей.

4.Все активы абсолютно делимы и совершенно ликвидны (т.е. всегда могут быть проданы на рынке по существующей цене).

5.Не существует трансакционных расходов.

6.Не принимаются во внимание налоги.

7.Все инвесторы принимают цену как экзогенно заданную ве­личину (т.е. они полагают, что их деятельность по покупке и про­даже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг).

8.Количество всех финансовых активов заранее определено и фиксировано.

Как легко заметить, многие из сформулированных предпосылок носят исключительно теоретический характер и не могут быть выпол­нены на практике.

Для понимания логики модели легче всего воспользоваться гра­фическим представлением (Рисунок 6.2). Ставится задача найти взаимо­связь между ожидаемой доходностью (у) и риском ценной бумаги (х), т.е. построить функцию у = f(x). Построение основывается на следующих очевидных рассуждениях:

· доходность ценной бумаги связана с присущим ей риском прямой связью;

· риск характеризу­ется некоторым показателем b;

· «средней» ценной бумаге, т.е. бу­маге, имеющей средние значения риска и доходности, соответствуют b=1 и доходность d_m;

· имеются безрисковые ценные бумаги со ставкой d_rf и b = 0.

Исходя из приведенных выше предпосылок доказывается, что ис­комая зависимость у = f(x) представляет собой прямую линию. Итак, мы имеем две точки с координатами (0, d_rf) и (1, d_m). Из курса геометрии известно, что уравнение прямой, проходящей через точки (х₁, у₁) и (х₂, у₂), задается формулой

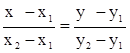(6.8)

Подставляя в формулу исходные данные, получим:

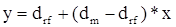(6.9)

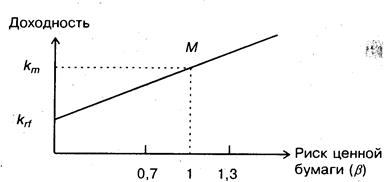
Рисунок 6.2. Логика представления модели CAPM

Имея в виду, что переменная х представляет собой риск, харак­теризуемый показателем b, а у – ожидаемую доходность d_ex, полу­чим следующую формулу, которая и представляет собой модель САРМ:

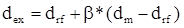(6.10)

где d_ex – ожидаемая доходность акций данной компании;

d_rf – доходность безрисковых ценных бумаг (в частности, в США берут за осно­ву государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка);

d_m – ожидаемая доходность в среднем на рынке ценных бумаг;

b – бета-коэффициент данной компании.

Показатель (d_m – d_rf) имеет вполне наглядную интерпретацию, представляя собой рыночную (т.е. в среднем) премию за риск вло­жения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпорации и пр.). Аналогично показатель (d_ex – d_rf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компа­нии. Модель САРМ означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск.

Модель САРМ позволяет прогнозировать доходность финансово­го актива. В свою очередь, зная этот показатель и имея данные об ожи­даемых доходах по этому активу, можно рассчитать его теоретическую стоимость. Не случайно поэтому модель САРМ называют еще моде­лью ценообразования финансовых активов.

Систематический риск в рамках модели САРМ измеряется с помощью b-коэффициентов (бета-коэффициентов). Каждый вид ценной бумаги имеет собственный b-коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя b рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуется в специ­альных справочниках. Для каждой компании b меняется с течением времени и зависит от многих факторов, в частности имеющих отношение к характеристике деятельности компании с позиции долгосроч­ной перспективы. Очевидно, что сюда относится, прежде всего, пока­затель уровня финансового левериджа, отражающего структуру ис­точников средств: при прочих равных условиях, чем выше доля заемного капитала, тем более рисковая компания и тем выше ее b[2].

Например, имеется совокупность показателей доходности по груп­пе компаний за ряд периодов {d_ij}, где: d_ij – показатель доходности i-й компании (i = 1,2,...,t) j-м периоде (j = 1,2,...,n). Тогда формула расчета b-коэффициента для любой i-й компании имеет вид:

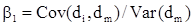(6.11)

где ;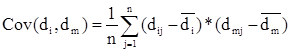

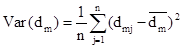
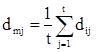– доходность в среднем на рынке ценных бумаг j-м периоде;

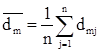– доходность в среднем на рынке ценных бумаг за все периоды;

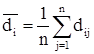– доходность ценных бумаг i-й компании в среднем за все периоды.

В целом по рынку ценных бумаг b-коэффициент равен единице; для отдельных компаний он колеблется около единицы, причем большинство b-коэффициентов находится в интервале от 0,5 до 2,0. Интерпретация b-коэффициента для акций конкретной компании заключается в следующем:

· b = 1 означает, что акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;

· b < 1 означает, что ценные бумаги данной компании менее риско­ванны, чем в среднем на рынке (так, b = 0,5 означает, что данная ценная бумага в два раза менее рискованна, чем в среднем на рынке);

· b > 1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке;

· увеличение b-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рискованными;

· снижение b-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся менее рискованными.

В качестве примера можно привести усредненные данные о b-коэффициентах ряда американских компаний в 1987–1991 гг.:

· наивысшие значения b-коэффициентов имели компании:

American Express – 1,5;

Bank America – 1,4;

Chrysler–1,4.

· средние значения b-коэффициентов имели компании:

Digital Equipment – 1,1;

Walt Disney – 0,9;

Du Pont – 1,0.

· наименьшие значения b-коэффициентов имели компании:

General Mills – 0,5;

Gillette – 0,6;

Southern California Edison – 0,5.

Следует отметить, что единого подхода к исчислению b-коэффи-циентов, в частности в отношении количества и вида исходных наблюдений, не существует. Так, известный американский банкирский дом «Merrill Lynch», занимающийся также и публикацией различных рыночных индикаторов, при расчете b-коэффициентов компаний в качестве d_m использует индекс S&P 500 и месячные данные о доход­ности компаний за пять лет, т.е. 60 наблюдений. Другая компания «Value Line», занимающаяся подобной деятельностью, ориентирует­ся на индекс курсов акций Нью-йоркской фондовой биржи (NYSE Composite Index), включающий данные о доходности обыкновенных акций более чем 1800 компаний, и использует 260 недельных на­блюдений.

С 1995 г. b-коэффициенты появились и на отечественном рынке ценных бумаг. Расчеты выполняются информационно-аналитическим агентством «Анализ, консультация и маркетинг» (АК&М), однако спи­сок компаний, как правило, не превышает полутора десятков, охваты­вая в основном предприятия энергетики и нефтегазового комплекса. Значения b-коэффициентов достаточно ощутимо варьируют. Так, в ян­варе 1997 г. нефтедобывающая отрасль имела b = 0,9313, а нефтехими­ческая – b = 0,1844. b-коэффициенты периодически публикуются в газете «Финансовые известия».

Пример: Расчет ожидаемой доходности финансового актива

Рассматривается целесообразность инвестирования в акции ком­пании А, имеющей b=1,6 или компании Б, имеющей b=0.9, если d_rf = 6%; d_m = 12%. Инвестиция делается в том случае, если доход­ность составляет не менее 15%.

Необходимые для принятия решения оценки можно рассчитать с помощью модели САРМ. По формуле (10) находим:

для компании А: d_ex = 6% + 1.6 * (12% – 6%) = 15.6%,

для компании Б: d_ex = 6% + 0.9 * (12% – 6%) = 11.4%.

Таким образом, наиболее целесообразной является инвестиция в акции компании А.

Для наглядности логика взаимосвязи рассмотренных показателей может быть объяснена с помощью графика, носящего название линии рынка ценных бумаг (Security Market Line, SML). График SML отражает линейную зависимость «доходность/риск» для конкретных ценных бумаг и выглядит следующим образом (Рисунок 6.3).

Важным свойством модели САРМ является ее линейность отно­сительно степени риска. Это дает возможность определять b-коэффициент портфеля как средневзвешенную b-коэффициентов входящих в портфель финансовых активов.

(6.12)

b_i – значение бета-коэффициента i-го актива в портфеле;

b_p – значение бета-коэффициента портфеля;

d_i – доля i-го актива в портфеле;

n – число различных финансовых активов в портфеле.

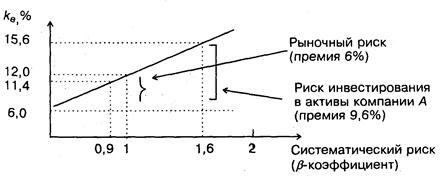
Рис. 6.3. График линии рынка ценных бумаг

Пример: Расчет b-коэффициента портфеля ценных бумаг

Портфель включает следующие активы:

• 12% акции компании А, имеющие b = 1;

• 18% акции компании В, имеющие b = 1,2;

• 25% акции компании С, имеющие b = 1,8;

• 45% акции компании D, имеющие b = 0,7.

Тогда b-коэффициент инвестиционного портфеля будет равен:

b_р= 0,12*1 + 0,18*1,2 + 0,25*1,8 + 0,45*0,7 = 1,10.

Обобщением понятия «линия рынка ценных бумаг» является линия рынка капитала (Capital Market Line, CML), отражающая зависимость (доходность/риск) для эффективных портфелей, которые, как правило, сочетают безрисковые и рисковые активы.

Линию рынка капитала можно использовать для сравнительного анализа портфельных инвестиций. Как следует из модели САРМ, каж­дому портфелю соответствует точка в квадранте на рис. 2. Возмож­ны три варианта расположения этой точки: на линии рынка капитала, ниже или выше этой линии. В первом случае портфель называется эффективным, во втором – неэффективным, в третьем – сверхэф­фективным.

Как отмечено выше, модель САРМ разработана исходя из ряда пред­посылок, часть из которых не выполняется на практике, например, налоги и трансакционные затраты существуют, инвесторы находятся в неравных условиях, в том числе и в отношении доступности инфор­мации и т.п. Поэтому модель не является идеальной и неоднократно подвергалась как критике, так и эмпирической проверке. Существуют различные точки зрения по поводу модели, поэтому приведем неко­торые наиболее типовые представления о современном состоянии этой теории из обзора, сделанного Ю.Бригхемом и Л.Гапенски:

· концепция САРМ, в основе которой лежит приоритет рыночного риска перед общим, является весьма полезной, имеющей фундаментальное значение в концептуальном плане. Модель логично отражает поведение инвестора, стремящегося максимизировать свой доход при заданном уровне риска и доступности данных;

· теоретически CAPM дает однозначное и хорошо интерпретируемое представление о взаимосвязи между риском и требуемой доход­ностью, однако она предполагает, что для построения связи должны использоваться априорные ожидаемые значения переменных, тогда как в распоряжении аналитика имеются лишь апостериорные факти­ческие значения. Поэтому оценки доходности, найденные с помощью модели, потенциально содержат ошибки;

· некоторые исследования, посвященные эмпирической провер­ке модели, показали на значительные отклонения между фактичес­кими и расчетными данными, что позволило ряду ученых подверг­нуть эту теорию серьезной критике. В частности, к ним относятся Ю. Фама и К. Френч, которые изучили зависимость между b-коэффциентами и доходностью нескольких тысяч акций по данным за пятьдесят лет. По мнению Бригхема и Гапенски, модель САРМ описывает взаимосвязи между ожидаемыми значениями перемен­ных, поэтому любые выводы, основанные на эмпирической провер­ке статистических данных, вряд ли правомочны и не могут опровер­гнуть теорию.

Тем не менее многие ученые понимают, что один из основных не­достатков модели заключается в том, что она является однофактор­ной. Указывая на этот недостаток, известные специалисты Дж. Уэстон и Т. Коуплэнд приводят такой образный пример. Представьте себе, что ваш маленький самолет не может совершить посадку из-за силь­ного тумана, и на вопрос диспетчерам о помощи вы получите инфор­мацию о том, что самолет находится в ста милях от посадочной поло­сы. Конечно, информация весьма полезна, но вряд ли достаточна для успешной посадки.

В научной литературе известны три основных подхода, альтерна­тивные модели САРМ: теория арбитражного ценообразования, тео­рия ценообразования опционов и теория преференций состояний в условиях неопределенности.

Наибольшую известность получила теория арбитражного ценообразования (Arbitrage Pricing Theory, APT). Концепция APT была предложена известным специалистом в области финансов, профессором Йельского университета Стивеном Россом. В основу модели за­ложено естественное утверждение о том, что фактическая доходность любой акции складывается из двух частей: нормальной, или ожидае­мой, доходности и рисковой, или неопределенной, доходности. Пос­ледний компонент определяется многими экономическими фактора­ми, например рыночной ситуацией в стране, оцениваемой валовым внутренним продуктом, стабильностью мировой экономики, инфля­цией, динамикой процентных ставок и др. Таким образом, модель может и должна включать множество факторов и в наиболее общем виде описывается следующей зависимостью:

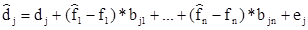(6.13)

где d_j – фактическая доходность j-й ценной бумаги;

d_j – ожидаемая доходность j-й ценной бумаги;

f_i – фактическое значение i-го экономического фактора;

f_i – ожидаемое значение i-го экономического фактора;

b_ji – чувствительность j-й ценной бумаги к i-му экономическому фактору;

e_j – влияние не включенных в модель специфических факторов на изменение доходности j-й ценной бумаги.

Данная модель обладает как достоинствами, так и недостатками. Прежде всего она не предусматривает таких жестких исходных предпосылок, которые свойственны модели САРМ. Количество и состав релевантных факторов определяются аналитиком и заранее не регламентируются. Фактическая реализация модели связана с привлечением достаточно сложного аппарата математической статистики, поэтому до настоящего времени теория APT носит достаточно теоретический характер. Тем не менее, главное достоинство этой теории, заключающееся в том, что доходность является функцией многих переменных, весьма привлекательна, и потому эта теория рассматрива­ется многими учеными как одна из наиболее перспективных.

Две другие альтернативы модели САРМ – теория ценообразова­ния опционов (Option Pricing Theory, OPT) и теория преференций со­стояний в условиях неопределенности (State-Preference Theory, SPT), – по тем или иным причинам еще не получили достаточного развития и находятся в стадии становления. По этой причине мы опускаем их рассмотрение в нашем курсе.