Дополним отношение строгого упорядочения Pуп свойством транзитивности. Назовем полученное отношение качественным порядком Pкач. Рассмотрим два примера такого отношения.
1) Пусть х, у – вещественные числа. Введем качественный порядок следующим соотношением:
хРкачу Û x > у + 1.
Очевидно, что в данном случае отношение Ркач асимметрично и транзитивно, но оно не является негатранзитивным. Покажем это.
Дополнение к введенному отношению определим как
х`Ркач у <=> х £ у + 1
Положим у = 0; х = 0.9; z = – 0.9. Тогда, очевидно, выполняются отношения (х, y) Î`Ркач ; (y, z) Î`Ркач ; (х, z) Ï Ркач. Т.е. условие негатранзитивности не выполняется.
Согласно рассмотренному примеру, а также доказанному ранее свойству транзитивности слабого порядка, можно сделать вывод, что асимметричное негатранзитивное отношение является транзитивным, но обратное не всегда верно.
2) Введем на множестве точек n-мерного евклидова пространства следующее отношение Par, называемое отношением Парето:
х, уÎРаr Û " i: хi ³ yi и $ j: хj > уj.
Отношение Парето называется также безусловным критерием предпочтения (БКП). Оно означает, что точка x по всем координатам имеет не меньшие значения, чем точка y и хотя бы по одной координате имеется строгое превосходство. В двумерном случае данное отношение можно изобразить графически. Возможны следующие ситуации:
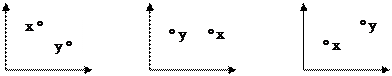 |
а) x1 < y1 б) x1 > y1 в) x1 < y1
x2 > y2 x2 = y2 x2 < y2
нет отношения Раr; есть отношение Раr, есть отношение Раr,
x лучше y; y лучше x.
Задание. Доказать, что отношение Раr является качественным порядком.
Также как и для Pуп и Pсл, на основе Pкач можно построить
производные от него отношения:
Iкач - отношение качественного безразличия;
хIкачу Û (x`Ркач у) и (у`Ркач х);
Rкач – нестрогий качественный порядок Rкач = Рd кач.
Качественный порядок также называют в литературе частичным порядком. Понятия же нестрого качественного и нестрого частичного порядков различны.
Помимо введенных выше специальных бинарных отношений дадим краткие определения некоторых других, часто встречающихся отношений.
Отношение Rчаст называется нестрогим частичным порядком, если оно рефлексивно, транзитивно и антисимметрично. Нестрогий частичный порядок можно определить по формуле Rчаст = Pкач È D.
Рефлексивное и транзитивное бинарное отношение называется предпорядком. Симметричный предпорядок является отношением эквивалентности, антисимметричный предпорядок – нестрогим частичным порядком.
В заключение изложения теории специальных бинарных отношений приведем сводную таблицу их свойств.
| Рефл. | Антирефл. | Симм. | Асимм. | Антисимм. | Транз. | Негатранз. | Полн. | Ацикл. | |
| Pуп | + | Å | |||||||
| Iуп | Å | Å | |||||||
| Rуп | + | Å | |||||||
| Pсл | + | Å | + | Å | + | ||||
| Iсл | Å | Å | Å | ||||||
| Rсл | + | Å | + | Å | |||||
| Pкач | + | Å | Å | + | |||||
| Rкач | + | Å | Å | ||||||
| Rчаст | Å | Å | Å |
В предлагаемой таблице использованы следующие обозначения:
Å – данным свойством отношение обладает по определению;
+ – это свойство вытекает из определения.
 2014-02-02
2014-02-02 595
595








