Операции над нечеткими отношениями

Объединение. Объединение двух отношений R₁ и R₂ обозначается R₁R₂ – отношение, с функцией принадлежности, определямое выражением: _R1R2(x, y) = max {_R1(x, y), _R2(x, y) }

Примеры:

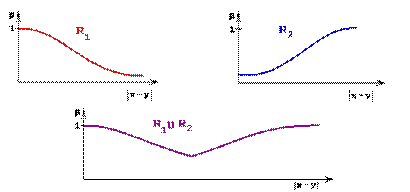
1. Ниже изображены отношения действительных чисел, содержательно означающие: x R₁ y – "числа x и y очень близкие", xR₂y – "числа x и y очень различны" и их объединение x R₁R₂ y – "числа x и y очень близкие или очень различные".

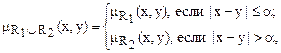
где  – такое значение | y – x |, что _R1(x, y) = _R2(x, y).

2.

Пересечение. Пересечение двух отношений R₁ и R₂ обо-значается R₁R₂ и определяется выражением:

_R1R2(x, y) = min { _R1(x, y), _R2(x, y) }.

Пример.

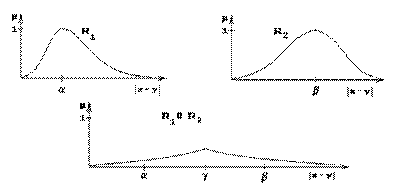
Выше изображены отношения: xR₁y, означающее "модуль разности | y – x | близок к ", xR₂y, означающее "модуль разности | y – x | близок к ", и их пересечение.

Алгебраическое произведение отношений. Алгебраическое произведение двух отношений R₁ и R₂ обозначается R₁R₂ и определяется выражением:

_R1R2 (x,y) = _R1 (x,y) _R2 (x,y)

Алгебраическая сумма отношений. Алгебраическая сумма двух отношений R₁ и R₂ обозначается R₁ + R₂ и опре-деляется выражением:

.

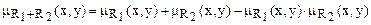Для введенных операций справедливы следующие свойства дистрибутивности:

R₁  (R₂  R₃) = (R₁  R₂)  (R₁ R₃),
R₁  (R₂  R₃) = (R₁  R₂)  (R₁  R₃),
R₁  (R₂  R₃) = (R₁R₂)  (R₁R₃),
R₁(R₂R₃) = (R₁R₂)(R_1R₃),
R₁ + (R₂  R₃) = (R₁ + R₂)  (R₁ + R₃),
R₁ + (R₂  R₃) = (R₁ + R₂)  (R₁ + R₃).

Дополнение отношения. Дополнение отношения R обозначается 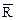и определяется функцией принадлежности:

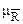(x,y) = 1 – _R(x,y).