Q = F (R),
где R = R1,…., Rm – производственные ресурсы
двухфакторная производственная функция:
Q = F (L; K)
Технологически эффективный способ производства
___
1. maxQ, 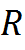
____
2. minR, Q
Пример производственной таблицы
| Использованное количество капитала | Использованное количество труда | |||||||
Анализ производства в краткосрочном периоде
 Средний продукт труда
Средний продукт труда
АРL=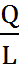
Предельный продукт труда
 |
МРL= =
= 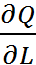 ,
,
Пример производственной таблицы
| Использованное количество капитала | Использованное количество труда | |||||||
Производство с одним переменным фактором (K=2)
| Использование труда (L) | Использование капитала (К) | Объем выпуска продукции (Q) | Предельный продукт труда (MPL) | Средний продукт труда (APL) |
| 9.67 | ||||
| 9.75 | ||||
| 9.4 | ||||
| 8.67 | ||||
| -4 | 6.5 |
Средний и Предельный продукты на графике
|
|
|
|
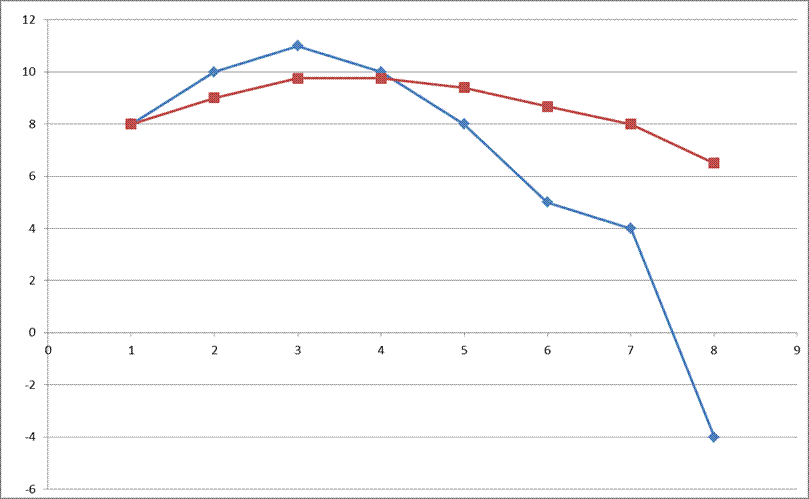
Снижение предельного продукта фактора производства отражает действие закона убывающей предельной производительности .
Важно:
1. Не путать закон убывающей производительности и изменения в качестве труда по мере увеличения его объема. Закон убывающей производительности действует вследствие ограничений на использование других постоянных факторов (например, техники), а не из-за снижения квалификации рабочих.
2. Н е следует путать убывающую производительность с отрицательной.
3. В законе ничего не говорится о том, когда начнет происходить уменьшение отдачи.
Рассмотренная промышленная ситуация описывает производственный процесс в условиях физического ограничения фиксированных затрат при добавлении к ним переменных затрат.
В рассмотренной ситуации к фиксированному капиталу добавляется больше труда.
Когда не работает ни один человек, ТР, или выпуск, равняется нулю.
Первый работник производит 8 единиц. Таким образом, его МР и АР равняются 8.
Когда используются два работника, их совместные усилия дают ТР, равный 18.
Таким образом, два человека, работающие вместе, могут произвести больше, чем если бы они работали по отдельности и их результаты складывались бы. (АР одного работника = 8, а АР двух работников = 9.)
МР второго работника больше, чем МР первого работника (МР второго работника = 10, т. е. больше МР первого работника, которое равно 8).
Эффект командной работы и специализации позволяет дополнительным работникам делать больший вклад по сравнению с работниками, которые добавлялись в производственный процесс перед ними - это возрастающая отдача.
По мере того, как добавляется все больше работников, остается все меньше возможностей для получения увеличивающейся отдачи через командную работу и специализацию. В определенный момент добавление работников приводит к уменьшению отдачи.
В конечном счете, может накопиться такое количество работников по сравнению с фиксированной мощностью, что они могут начать вмешиваться в деятельность друг друга, что приведет к отрицательной маржинальной отдаче и к снижению валового продукта.
Четыре стадии производства в коротком периоде
  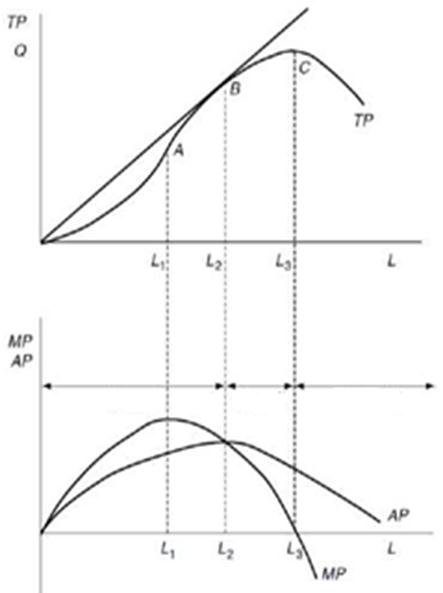
| I стадия. Фиксированные затраты в значительной степени недоиспользуются; увеличение затрат труда способствует все более полному использованию капитала - предельная и общая производительность труда растут, при этом МР > АР. В точке а - maxMP. Совокупный продукт возрастает медленнее, чем использованное количество переменного фактора II стадия. В еличина предельного продукта уменьшается. В точке В – maxAP, МР = АР. Cовокупный продукт растет быстрее, чем использованное количество переменного фактора |
  
| III стадия. МР < АР, в результате чего совокупный продукт растет медленнее затрат переменного фактора. В точке С – maxTP, MP=0 IV стадия. МР < 0. Достигнута максимальная производительность фиксированных затрат; дополнительные единицы труда приводят к сокращению выработки. В результате прирост переменного фактора L приводит к уменьшению выпуска совокупной продукции |
Анализ производства в долгосрочном периоде
| Исп. количество капитала | Использованное количество труда | |||||||
 18 18
|  29 29
|  39 39
|   52 52
|  52 52
| ||||
 29 29
|  41 41
|  52 52
|  64 64
|  73 73
| ||||
 39 39
|  52 52
|  60 60
|  73 73
| |||||
 52 52
|  73 73
| |||||||
Изокванта для Q= 52
|
|
|
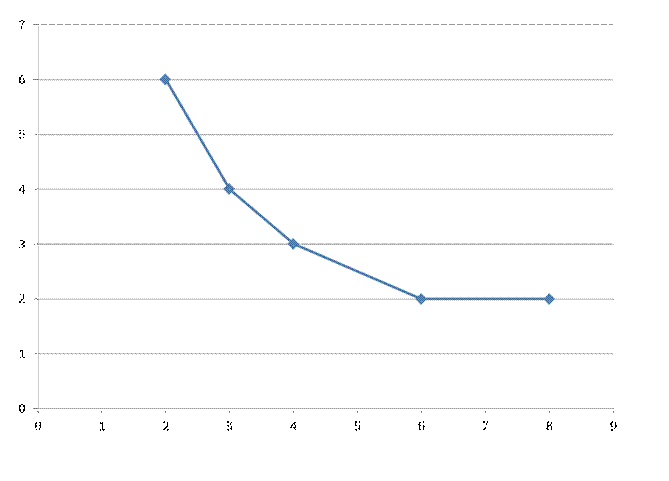
Непрерывная производственная функция, в которой затраты предполагаются полностью делимыми. Здесь изокванта выглядит как сглаженная версия изокванты, изображенной выше
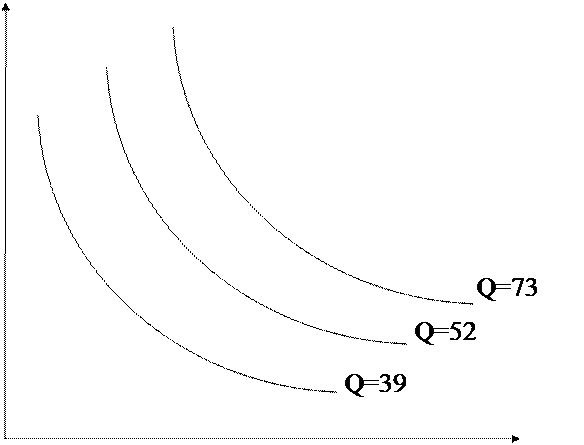 |
 2014-02-02
2014-02-02 355
355







