Формальные свойства производственных функций

Производственная функция f(x₁, x₂) определена при х₁≥0, х₂≥0. ПФ должна удовлетворять ряду (для каждой конкретной ПФ – своему) свойств:

1. ;

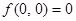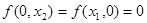; - без ресурсов нет выпуска, при отсутствии хотя бы одного из ресурсов нет выпуска.

2. 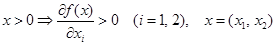; - с ростом затрат хотя бы одного ресурса объем выпуска растет, и с ростом затрат одного ресурса при неизменном количестве другого ресурса объем выпуска растет.

3. ;

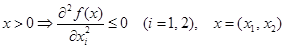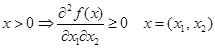;- с ростом затрат одного (i -го) ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу i -го ресурса не растет (закон убывающей эффективности), при росте одного ресурса предельная эффективность другого ресурса возрастает. (график Г ПФ есть поверхность, расположенная в неотрицательном ортанте 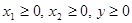трехмерного пространства Ох₁х₂у и выпуклая вверх.)

4. 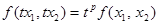. - ПФ является однородной функцией (ОФ) степени p>0. При p>1 с ростом масштаба производства в t раз (число t>1), т.е. с переходом от вектора х к вектору tx, объем выпуска возрастает в t^p (>t) раз, т.е. имеет рост эффективности производства от роста масштаба производства. При p<1 имеем падание эффективности производства от роста масштаба производства. При p=1 имеем постоянную эффективность производства при росте его масштаба.

Для ПФКД 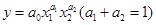свойства 1-4 выполняются.

Для ЛПФ 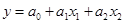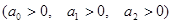свойства 1 (при 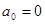) и свойство 4 не выполняются.

Множество (линия) l_q уровня 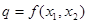(0<q – действительное число) ПФ 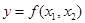называется изоквантой ПФ. Иными словами, линия уровня q – это множество точек, в котором ПФ постоянна и равна q.

Различные наборы 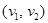и 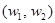затрачиваемых (используемых) ресурсов, принадлежащие одной и той же изокванте l_q (т.е. 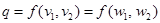), дают один и тот же объем выпуска q. Изокванта есть линия, расположенная в неотрицательном ортанте 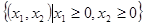двумерной плоскости Ох₁х₂.