2014-02-02
568
Предельные (маржинальные) и средние значения
Пусть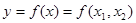 
– ПФ. Дробь
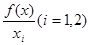
называется средней производительностью i -го ресурса (фактора производства) (СПФ) или средним выпуском по i -му ресурсу (фактору производства). Символика: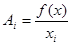 
.
Напомним, что в случае двухфакторной ПФКД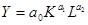 
для средних производительносте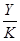й 
и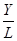 
основного капитала и труда были использованы соответственно термины капиталоотдача и производительность труда. Эти термины используют и применительно к любым двухфакторным ПФ, у которых 
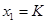и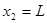 
.
Пусть 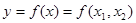– ПФ. Ее первая частная производная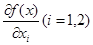 
называется предельной (маржинальной) производительностью i -го ресурса (фактора производства) (ППФ) или предельным выпуском по i -му ресурсу (фактору производства). Символика: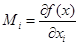 
.
Обозначим символами 
и 
;
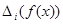
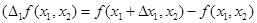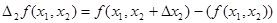соответственно, приращение переменной 
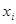и соответствующее ей частное приращение ПФ f(x). При малых имеем приближенное равенство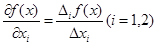 
.
Следовательно, ППФ (приближенно) показывает, на сколько единиц увеличится объем выпуска у, если объем затрат 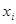i -го ресурса вырастает на одну (достаточно малую) единицу при неизменных объемах другого затрачиваемого ресурса. Здесь предельную величину 
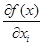(т.е. ППФ) целесообразно интерпретировать, используя близкое к ней отношение малых конечных величин, т.е. 
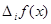и . Отмеченное обстоятельство является ключевым для понимания экономического смысла ППФ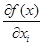. С другими предельными величинами следует поступать аналогичным образом.
