Эмпирическая функция распределения

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F_n(x), определяющую для каждого значения х относительную частоту события x<х, т.е. F_n(x)=n_x/n, где n_x – число вариант меньших х, n – объем выборки.

Из определения следует, что эмпирическая функция

Из определения эмпирической функции распределения следует, что она обладает всеми свойствами функции распределения:

1. 0£F_n(x)£1.

2. F_n(x) - неубывающая функция.

3. Если х₁ – наименьшая варианта, а х_к – наибольшая варианта, то F_n(x)=0 при x£x₁, и F_n(x)=1 при х>x_к.

Теорема 7.2.1. (Гливенко – Кантелли).

Эмпирическая функция распределения F_n(x) сходится по вероятности к теоретической функции распределения F(x), т.е. для любого хÎR и для любого e>0

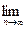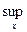P(½F_n(x)–F(x)½<e)=1.

Доказательство. Доказательство теоремы Гливенко-Кантелли является довольно сложным, поэтому докажем следующий её упрощенный вариант. «При любом ε>0 верно

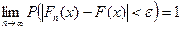для любого х». По определению F_n(x_k)=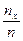, где n_x число вариант меньших х_k. Рассмотрим наблюдения как n независимых испытаний Бернулли, в каждом из которых возможны два исхода: 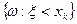или 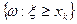. Вероятности этих событий соответственно равны p=P(x<x_k)=F_x(x_k) и q=P(x³x_k)=1-F_x(x_k). Событие {w:x<x_k} будем называть успехом, а n_x - число успехов в n независимых испытаниях Бернулли. Тогда математическое ожидание равно Мn_x=np, и дисперсия равна Dn_x=npq. Отсюда получим

.

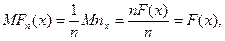
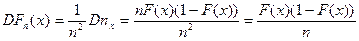В силу неравенства Чебышева для любого фиксированного e>0 верна оценка

P(½F_n(x)–F(x)½³e)£,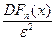

поэтому P(½F_n(x)–F(x)½³e)£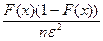®0 при n®µ,

откуда следует утверждение теоремы, что при n®¥ F_n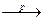(x)F(x).

Смысл теоремы Гливенко-Кантелли заключается в том, что при увеличении объема выборки у эмпирической функции распределения исчезают свойства случайности, и она приближается к теоретической функции распределения.
Эмпирическая функция распределения служит оценкой функции распределения генеральной совокупности.

График эмпирической функции распределения есть неубывающая ступенчатая кривая со скачками равными 1/n в точках вариационного ряда. Если m точек вариационного ряда совпадают и равны x_i, то скачок в точке x_i равен m/n.

Например, задана таблица наблюдений за значениями случайной величины x:

xi
ni
wi	0,75	0,2	0,05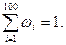

Эмпирическая функция распределения имеет вид:

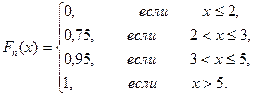
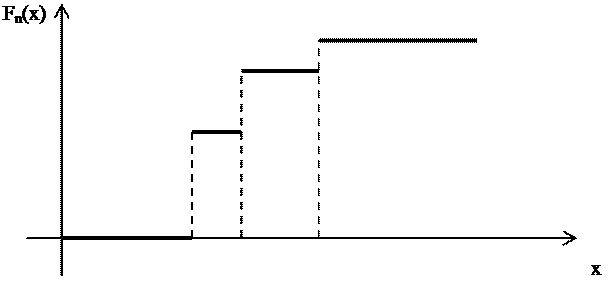
Рис.7.2.1.

Задача Пусть х₁,х₂,...,х_n - выборка независимых наблюдений из непрерывной генеральной совокупности с функцией распределения F(x) и плотностью распределения f(x). Найти функции распределения и плотности распределения крайних членов вариационного ряда: x_min и x_max.

Решение. Из определения функции распределения следует, что

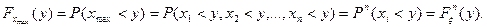
Тогда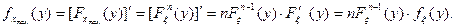

Аналогично,

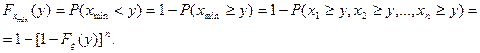
Отсюда получаем функцию плотности