Пример 4.
Даны комплексные числа  ,
, 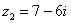 . Найти частное
. Найти частное 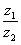 .
.
Составим частное:
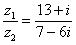
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем формулу 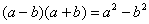 и смотрим на наш знаменатель:
и смотрим на наш знаменатель: 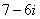 . В знаменателе уже есть
. В знаменателе уже есть 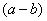 , поэтому сопряженным выражением в данном случае является
, поэтому сопряженным выражением в данном случае является 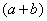 , то есть
, то есть 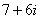
Согласно правилу, знаменатель нужно умножить на 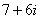 , и, чтобы ничего не изменилось, домножить числитель на то же самое число
, и, чтобы ничего не изменилось, домножить числитель на то же самое число 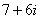 :
:
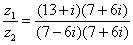
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой 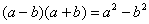 (помним, что
(помним, что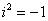 и не путаемся в знаках!!!).
и не путаемся в знаках!!!).
Подробно:

Если взять произвольных два числа, то в результате деления почти всегда получатся дроби, что-нибудь вроде 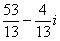 .
.
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: 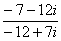 .
.
Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: 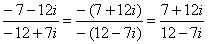 . (правильный ответ:
. (правильный ответ: 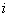 )
)
 2014-02-02
2014-02-02 1024
1024








