Тема 8. Комплексные числа и действия с ними

Вычисление высоты тетраэдра (параллелепипеда) (рис. 2.10).

Вычислим объем тетраэдра двумя способами:

с одной стороны,

,

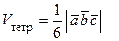с другой стороны,

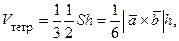
отсюда (высота параллелепипеда такая же);

3) Условие компланарности векторов (теорема 2.1):

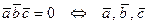– компланарны.

Ввиду обширности курса и нашего небольшого количества занятий тема, приводимая ниже: Тема 8. Комплексные числа и действия с ними - дается для самостоятельного ознакомления.

1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

Сначала вспомним «обычные» школьные числа. В математике они называются множеством действительных чисел и обозначаются буквой 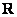(в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой).

Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень разная – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой обязательно соответствует некоторое действительное число.

Понятие комплексного числа

Комплексное число «в жизни» предствить очень трудно– это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число.

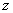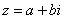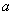Комплексным числом называется число вида , где и 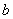– действительные числа, 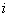– так называемая мнимая единица.

Число 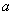называется действительной частью ( ) комплексного числа 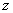, число 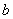называется мнимой частью ( 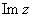) комплексного числа .

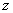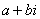– это ЕДИНОЕ ЧИСЛО, а не сложение.

Буквой 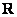принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой 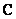. Поэтому на чертеже следует поставить букву 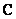, обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей:
– действительная ось
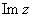– мнимая ось

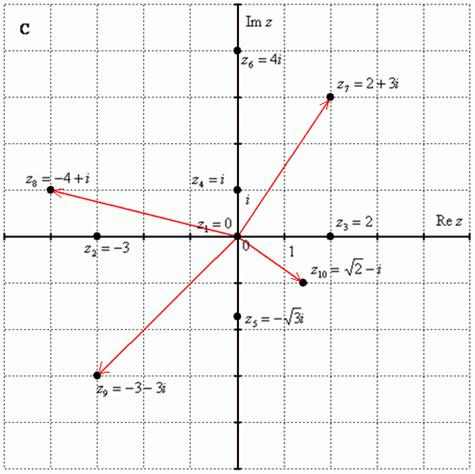
Задание: Постройте на комплексной плоскости следующие комплексные числа:
, ,
, ,
, , ,

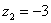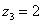
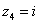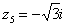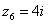
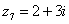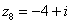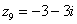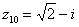
8.2.Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел