2014-02-02
511
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ ВЗВЕШЕННАЯ
ДРУГИЕ ВИДЫ СРЕДНЕЙ
Средняя геометрическая:
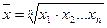- невзвешенная
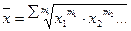- взвешенная
Средняя квадратическая:
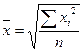- невзвешенная
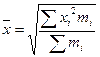- взвешенная
| Область | Валовый сбор, тыс. т | Урожайность, ц/га |
| 0,5 | 16,1 9,5 4,8 10,9 7,0 |
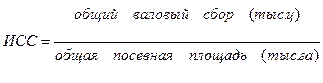
общий валовый сбор - 
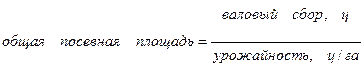
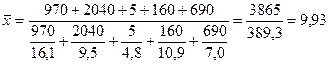ц/га
|
 | |||||
 | |||||
 |
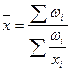
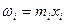
валовый посевная урожайность
сбор площадь (вес)
1-й сотрудник – 8 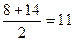мин 
мин
2-й сотрудник 14 мин
За 1 ч: 1-й -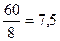 
заказов, 2-й - 
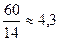заказа, 1-й + 2-й = 11,8 заказов
Заменим t1 и t2 средним значением: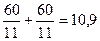 
заказов
Среднее время выполнения одного заказа занижено!
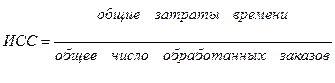
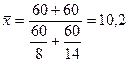мин
|
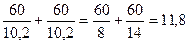
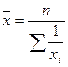
Соотношение между средними: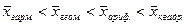 
Ряды распределения.
Ряд распределения – упорядоченные по определенному варьирующему признаку однородные единицы совокупности.
Атрибутивный ряд распределения – ряд, построенный по качественному признаку. Число групп атрибутивного ряда распределения равно числу градаций признака.
Вариационный ряд распределения – ряд, построенный по количественному признаку. Он состоит из значений признака и частоты значений или частости. Различают дискретные и интервальные ряды распределения.
ПОКАЗАТЕЛИ ВАРИАЦИИ
1. Размах вариации:
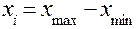
2. Среднее значение признака:
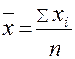
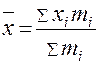
3. Среднее линейное отклонение:
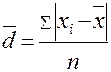
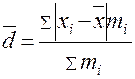
4. Среднее квадратическое отклонение:
(
)
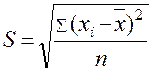
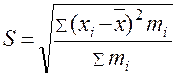
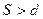5.Дисперсия:
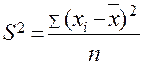
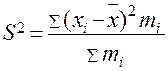
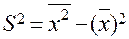, где 
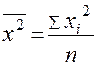или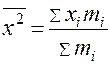
6. Коэффициент вариации (относительная колеблемость):
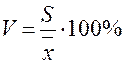
Ряды динамики.
Ряды динамики – это последовательность значений какого-либо показателя, упорядоченная в хронологическом порядке.
Ряд динамики состоит из значений времени и значений показателя – уровней ряда.
Различают моментные и интервальные ряды динамики.
Уровни рядов динамики могут представлять собой абсолютные, относительные и средние величины. Абсолютные величины – непосредственно наблюдаемые значения, относительные или средние величины – результат вычислений (такие ряды называют производными).
Интервальные ряды динамики обладают свойством аддитивности – их уровни можно суммировать.
