Решение.
Напряженность магнитного поля соленоида бесконечной длины 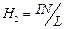 . Напряженность магнитного поля соленоида конечной длины
. Напряженность магнитного поля соленоида конечной длины 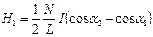 . Т.е.
. Т.е. 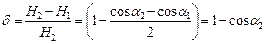 , т.к.
, т.к. 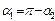 и
и 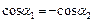 Из рис. видно, что
Из рис. видно, что 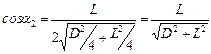 , получаем
, получаем 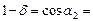
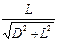 . Возведем в квадрат правую и левую часть равенств и получим
. Возведем в квадрат правую и левую часть равенств и получим 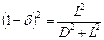 и
и 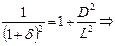
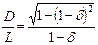 и
и 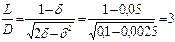 .
.
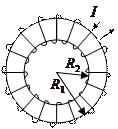 Тороид – кольцевая катушка, намотанная на сердечник, имеющая форму тора. Если витки расположены вплотную или очень близко друг к другу, то тороид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на средней линии тороида, а плоскости ортогональны ей.
Тороид – кольцевая катушка, намотанная на сердечник, имеющая форму тора. Если витки расположены вплотную или очень близко друг к другу, то тороид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на средней линии тороида, а плоскости ортогональны ей.
Для контура, совпадающего с силовой линией внутри тороида, из закона полного тока следует: 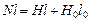 , где N- число витков тороида,
, где N- число витков тороида, 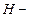 .напряженность магнитного поля в сердечнике,
.напряженность магнитного поля в сердечнике, 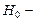 напряженность поля в зазоре,
напряженность поля в зазоре, 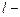 длина сердечника,
длина сердечника, 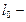 длина зазора.
длина зазора.
Магнитное поле целиком локализовано внутри его объема: 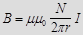 ,
, 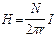 , где N- число витков тороида. Поле вне тороида отсутствует.
, где N- число витков тороида. Поле вне тороида отсутствует.
В случае тонкого тороида диаметр витков 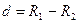 мал по сравнению с радиусом средней линии
мал по сравнению с радиусом средней линии и в пределах площади витка магнитное поле тороида можно считать однородным
и в пределах площади витка магнитное поле тороида можно считать однородным 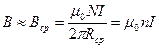 , где
, где 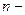 число обмотки тороида, приходящихся на единицу длины его средней линии. Если неограниченно увеличивать
число обмотки тороида, приходящихся на единицу длины его средней линии. Если неограниченно увеличивать 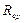 , то в пределе получится бесконечно длинный соленоид.
, то в пределе получится бесконечно длинный соленоид.
Магнитный поток через поверхность, ограниченную замкнутым контуром, наз. потокосцеплением этого контура.
Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками равномерно обмотанного соленоида или тороида, определяется по формуле: 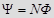 , где
, где 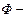 магнитный поток через один виток, N- число витков соленоида или тороида.
магнитный поток через один виток, N- число витков соленоида или тороида.
Потокосцепление контура, обусловленное магнитным полем тока в самом контуре, наз. потокосцеплением самоиндукции.
Потокосцепление контура, обусловленное магнитным полем тока, идущего в другом контуре, наз. потокосцеплением взаимной индукции этих двух контуров.
Найдем потокосцепление самоиндукции тонкого тороида.
Магнитный поток сквозь тороид 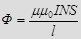 , если тороид имеет воздушный (или заполненный веществом с магнитной проницаемостью
, если тороид имеет воздушный (или заполненный веществом с магнитной проницаемостью 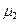 ) зазор
) зазор 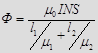 , где
, где 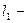 длина железного сердечника,
длина железного сердечника, 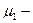 его магнитная проницаемость,
его магнитная проницаемость, 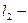 длина воздушного зазора.
длина воздушного зазора.
Задача 8. Определить индукцию и напряженность магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей 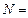 200 витков, идет ток силой
200 витков, идет ток силой 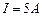 . Внешний диаметр тороида
. Внешний диаметр тороида 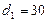 см, внутренний -
см, внутренний - 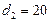 см.
см.
|

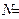 200 витков
200 витков
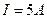
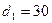 см
см

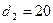 см
см
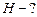 ,
,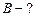
получим  . Силовая линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова, следовательно
. Силовая линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова, следовательно 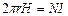 . Отсюда
. Отсюда 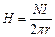 . Для средней линии тороида
. Для средней линии тороида 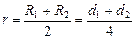 ,
, 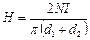 .
. 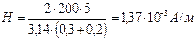 ; магнитная индукция в вакууме
; магнитная индукция в вакууме 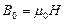 ,
, 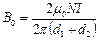 .
. 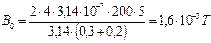 .
.
Ответ: 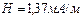 ;
; 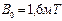 .
.
 2014-02-02
2014-02-02 2757
2757

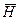 вдоль силовой линии поля
вдоль силовой линии поля 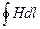 . Из условия симметрии следует. Что силовые линии тороида представляют собой окружности и что во всех точках силовой линии численное значение напряженности одно и то же. Пусть
. Из условия симметрии следует. Что силовые линии тороида представляют собой окружности и что во всех точках силовой линии численное значение напряженности одно и то же. Пусть 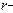 радиус окружности, совпадающей с силовой линией, вдоль которой вычисляется циркуляция, т.е.
радиус окружности, совпадающей с силовой линией, вдоль которой вычисляется циркуляция, т.е. 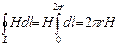 . С другой стороны, в соответствии с законом полного тока
. С другой стороны, в соответствии с законом полного тока 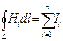 .Приравняв правые части равенства,
.Приравняв правые части равенства, 






