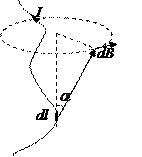 Для ферромагнитных тел
Для ферромагнитных тел 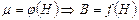 . При решении задач, где требуется знать зависимость
. При решении задач, где требуется знать зависимость  , необходимо пользоваться графиком, приведенном в приложениях задачников по физике или справочными таблицами.
, необходимо пользоваться графиком, приведенном в приложениях задачников по физике или справочными таблицами.
Количественный закон, описывающий создаваемую прямым проводником с током магнитную индукцию, пытались найти французы Жан Батист Био (1774-1862) и Феликс Савар (1793-1841). Они применили метод крутильных колебаний: если магнитную стрелку, помещенную в магнитное поле, слегка отклонить от положения равновесия, она будет колебаться с периодом, зависящим от величины действующей на стрелку силы. В итоге Био и Савар установили, что индукция магнитного поля прямого провода с током ослабевает обратно пропорционально расстоянию от него. Известный французский астроном, физик и математик Пьер Симон Лаплас (1749-1827), узнав из беседы с Био об этих результатах, предположил: если разбить провод с током на малые отрезки 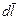 (элементы тока, аналоги точечных зарядов в электростатике), то каждый такой элемент должен создавать магнитную индукцию
(элементы тока, аналоги точечных зарядов в электростатике), то каждый такой элемент должен создавать магнитную индукцию  , которая будет изменяться обратно пропорционально квадрату расстояния.
, которая будет изменяться обратно пропорционально квадрату расстояния.

Закон Био-Савара-Лапласа устанавливает величину и направление вектора магнитной индукции dB в произвольной точке С магнитного поля, создаваемого элементом 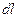 проводника с током I:
проводника с током I: 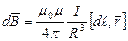 , где
, где 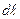 - вектор, по модулю равный длине
- вектор, по модулю равный длине 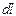 элемента проводника и совпадающий по направлению с током,
элемента проводника и совпадающий по направлению с током, 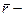 радиус – вектор, проведенный из элемента
радиус – вектор, проведенный из элемента 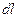 проводника в точку C магнитного поля,
проводника в точку C магнитного поля, 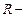 модуль радиуса вектора
модуль радиуса вектора 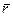 .
.
В скалярной форме (модуль вектора 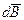 ):
): 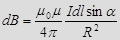 , где
, где 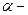 угол между векторами
угол между векторами 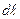 и
и 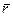 .
.
Направление 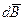 перпендикулярно
перпендикулярно  и
и 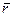 , т.е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта даст направление
, т.е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта даст направление 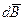 , если поступательное направление винта соответствует направлению тока элементе.
, если поступательное направление винта соответствует направлению тока элементе.
Принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: 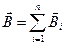 .
.
В частном случае наложения двух полей 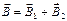 , а абсолютное значение вектора магнитной индукции
, а абсолютное значение вектора магнитной индукции 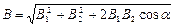 , где
, где 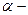 угол между векторами
угол между векторами 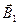 и
и 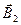 .
.
Применение закона Био-Савара-Лапласа для расчета полей:
1. 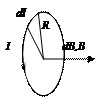 Магнитное поле в центре кругового проводника с током. Все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Поэтому сложение векторов
Магнитное поле в центре кругового проводника с током. Все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Поэтому сложение векторов 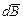 можно заменить сложением их модулей. Т.к. все элементы проводника перпендикулярны радиусу-вектору
можно заменить сложением их модулей. Т.к. все элементы проводника перпендикулярны радиусу-вектору 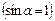 и расстояние всех элементов проводника до центра кругового тока одинаково и равно
и расстояние всех элементов проводника до центра кругового тока одинаково и равно 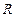 , то
, то 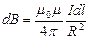 . Тогда
. Тогда 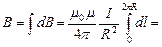
 . Получаем
. Получаем 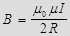 , где
, где 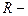 радиус кривизны проводника.
радиус кривизны проводника.
2. 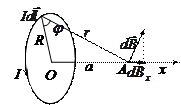 Магнитное поле на оси кругового тока. Выберем элемент тока
Магнитное поле на оси кругового тока. Выберем элемент тока 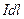 в точке А он создаст поле
в точке А он создаст поле 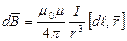 . В силу симметрии суммарный вектор
. В силу симметрии суммарный вектор 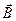 направлен вдоль оси
направлен вдоль оси 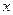 , т.е. для нахождения модуля вектора надо сложить проекции всех векторов
, т.е. для нахождения модуля вектора надо сложить проекции всех векторов 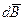 на ось
на ось 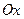 .
. 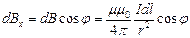 . Интегрируя это выражение по всем
. Интегрируя это выражение по всем  и учитывая, что
и учитывая, что 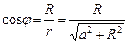 , получаем
, получаем 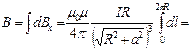
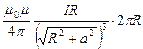 , т.е.
, т.е.  , где
, где 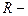 радиус кругового контура с током,
радиус кругового контура с током, 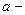 расстояние от точки, где ищется напряженность, до плоского контура.
расстояние от точки, где ищется напряженность, до плоского контура.
3. 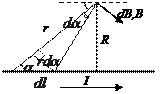
 Магнитное поле прямого тока – тока, текущего по тонкому прямому проводнику бесконечной длины. В произвольной точке А, удаленной от оси проводника на расстояние
Магнитное поле прямого тока – тока, текущего по тонкому прямому проводнику бесконечной длины. В произвольной точке А, удаленной от оси проводника на расстояние 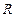 , векторы
, векторы  от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов
от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов 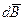 можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол
можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол 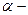 угол между векторами
угол между векторами  и
и 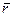 , выразив через него все остальные величины:
, выразив через него все остальные величины: 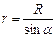 ,
, 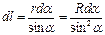 (т.к. угол
(т.к. угол 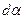 очень мал), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
очень мал), получим, что магнитная индукция, создаваемая одним элементом проводника, равна 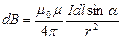
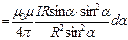
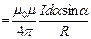 . Т.к. угол для всех элементов изменяется в пределах от
. Т.к. угол для всех элементов изменяется в пределах от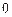 до
до , то
, то 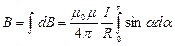
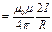 . Магнитная индукция
. Магнитная индукция 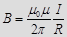 .
.
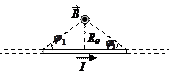 Пример: найдем магнитную индукцию поля, создаваемого отрезком проводника. По закону Био-Савара-Лапласа
Пример: найдем магнитную индукцию поля, создаваемого отрезком проводника. По закону Био-Савара-Лапласа 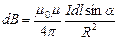 . Радиус-вектор направлен от элемента провода к точке, в которой вычисляется индукция поля. Выразим длину элемента проводника
. Радиус-вектор направлен от элемента провода к точке, в которой вычисляется индукция поля. Выразим длину элемента проводника  через
через  . По чертежу
. По чертежу 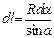
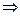
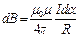 , но
, но 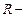 величина переменная, зависящая от
величина переменная, зависящая от 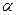 :
: 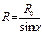
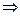
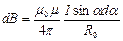 .
. 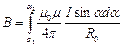
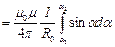 или
или 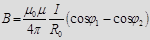 .
.
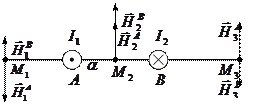 При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция
При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция  и
и 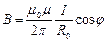
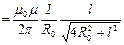 , где
, где 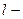 длина отрезка проводника.
длина отрезка проводника.
Пример. По двум прямолинейным параллельным противоположно направленным бесконечно длинным проводникам, находящимся на расстоянии 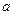 , текут токи
, текут токи 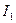 и
и 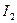 . Найти напряженность магнитного поля, вызванного этими токами, в точках
. Найти напряженность магнитного поля, вызванного этими токами, в точках 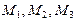 . Расстояния от проводников до точек равны:
. Расстояния от проводников до точек равны: 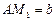 ,
, 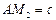 ,
,  . Точки лежат на прямой, соединяющей проводники.
. Точки лежат на прямой, соединяющей проводники.
РЕШЕНИЕ. Согласно принципу суперпозиции напряженности 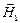 ,
, 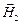 и
и 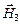 магнитного поля в точках
магнитного поля в точках 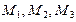 складываются из напряженностей, создаваемых токами
складываются из напряженностей, создаваемых токами 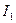 и
и 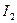 .
.  ,
, 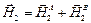 и
и 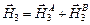 . Напряженность
. Напряженность 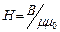 , а магнитная индукция проводника
, а магнитная индукция проводника 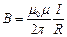 , тогда
, тогда  , где
, где 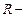 расстояние от проводника с током до точки, где определяется напряженность. Тогда
расстояние от проводника с током до точки, где определяется напряженность. Тогда 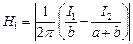 ,
, 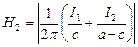 ,
, 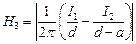
 2014-02-02
2014-02-02 1766
1766
