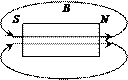
Французский физик Доминик Франсуа Араго (1786-1853) на заседании Парижской академии наук рассказал об опытах Эрстеда и повторил их. Араго предложил естественное, как всем казалось, объяснение магнитного действия электрического тока: проводник в результате протекания по нему электрического тока превращается в магнит. На демонстрации присутствовал другой академик, математик Андре Мари Ампер. Он предположил, что суть вновь открытого явления – в движении заряда, и решил сам провести необходимые измерения. Ампер был уверен, что замкнутые токи эквивалентны магнитам. 24 сентября 1820 г. он подключил к вольтову столбу две проволочные спирали, которые превратились в магниты.
Т.о. катушка с током создает такое же поле, что и полосовой магнит. Ампер создал прообраз электромагнита, обнаружив, что стальной брусок, помещенный внутрь спирали с током, намагничивается, многократно усиливая магнитное поле. Ампер предположил, что магнит представляет собой некоторую систему внутренних замкнутых токов и показал (и на основе опытов, и помощью расчетов), что малый круговой ток (виток) эквивалентен маленькому магнитику, расположенному в центре витка перпендикулярно его плоскости, т.о. всякий контур с током можно заменить магнитом бесконечно малой толщины.
|
|
|
Гипотеза Ампера, что внутри любого магнита существуют замкнутые токи, наз. гипотезой о молекулярных токах и легла в основу теории взаимодействия токов – электродинамики.
На проводник с током, находящийся в магнитном поле, действует сила, которая определяется только свойствами поля в том месте, где расположен проводник, и не зависит от того, какая система токов или постоянных магнитов создала поле. Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы.
Закон Ампера: сила, действующая на элемент длины проводника с током I, помещенного в магнитное поле 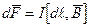 ,
,
где  сила,
сила, 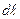 - вектор элемента длины проводника
- вектор элемента длины проводника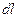 , проведенный в направлении тока.
, проведенный в направлении тока.
Модуль магнитной силы: 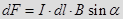 , где
, где 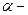 угол между
угол между 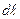 и
и 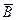 .
.
Следовательно, когда проводник расположен вдоль линий поля 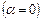 , магнитная сила отсутствует.
, магнитная сила отсутствует.
Направление вектора 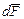 может быть найдено по общим правилам векторного произведения. В простейшем случае, когда проводник с током и поле взаимно перпендикулярны
может быть найдено по общим правилам векторного произведения. В простейшем случае, когда проводник с током и поле взаимно перпендикулярны 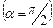 , для определения направления магнитной силы можно воспользоваться правилом левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор
, для определения направления магнитной силы можно воспользоваться правилом левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор 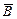 , а четыре вытянутых пальцев расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
, а четыре вытянутых пальцев расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
|
|
|
 , где
, где  число свободных электронов в единице объема проводника (концентрация частиц),
число свободных электронов в единице объема проводника (концентрация частиц),  - заряд электрона,
- заряд электрона,  - скорость упорядоченного движения электронов,
- скорость упорядоченного движения электронов, 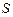 - площадь поперечного сечения проводника.
- площадь поперечного сечения проводника.
В отличие от кулоновских сил, которые являются центростремительными, сила Ампера не является центральной. Она направлена перпендикулярно к линиям магнитной индукции.
Закон Ампера может быть использован для определения модуля вектора магнитной индукции. Модуль вектора индукции в данной точке однородного магнитного поля равен наибольшей силе, которая действует на помещенный в окрестности данной точки проводник единичной длины, по которому протекает ток в единицу силы тока: 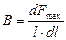 . Значение
. Значение  достигается при условии, что проводник расположен перпендикулярно к линиям индукции.
достигается при условии, что проводник расположен перпендикулярно к линиям индукции.
Закон Ампера применяется для определения силы взаимодействия двух токов.
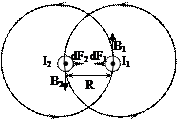
Между двумя параллельно расположенными бесконечно длинными проводниками, по которым протекают постоянные токи, возникает сила взаимодействия. Проводники с одинаково направленными токами притягиваются, с противоположно направленными токами – отталкиваются.
Сила взаимодействия, приходящаяся на единицу длины каждого из параллельных проводников, пропорциональна величинам токов  и
и 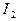 и обратно пропорциональна расстоянию между R между ними.
и обратно пропорциональна расстоянию между R между ними.  Такое взаимодействие проводников с параллельными токами объясняется правилом левой руки. Модуль силы, действующий на два бесконечных прямолинейных тока
Такое взаимодействие проводников с параллельными токами объясняется правилом левой руки. Модуль силы, действующий на два бесконечных прямолинейных тока  и
и 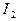 , расстояние между которыми равно R:
, расстояние между которыми равно R:
 , т.е.
, т.е.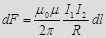 .
.
В неоднородном магнитном поле на контур с током действует сила 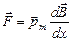 , где
, где 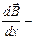 изменение
изменение 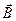 , рассчитанное на единицу длины вдоль направления, совпадающего с направлением
, рассчитанное на единицу длины вдоль направления, совпадающего с направлением 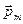 .
.
Сила 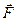 втягивает магнитный диполь в область больших значений магнитной индукции.
втягивает магнитный диполь в область больших значений магнитной индукции.
Задача 3. Определить степень неоднородности магнитного поля 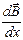 , если максимальная сила, действующая на точечный магнитный диполь
, если максимальная сила, действующая на точечный магнитный диполь  . Магнитный момент точечного диполя
. Магнитный момент точечного диполя 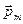 =2 мА?м2.
=2 мА?м2.
Дано: Решение:
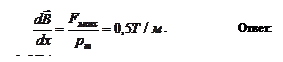
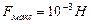 ,
, 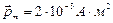
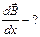
 2014-02-02
2014-02-02 10448
10448
