Прямые на плоскости и плоскости в пространстве

Продемонстрируем, как теория линейных систем иллюстрируется геометрическими примерами.

Рассмотрим множество точек плоскости XOY. Как известно, каждая точка на плоскости может быть задана с помощью двух декартовых координат 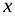и 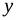, которые являются координатами проекций точки на координатные оси.

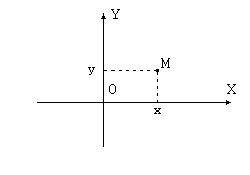
Простейшей плоской кривой является прямая – геометрическое место точек, соединив любые две из которых, мы получим отрезок, параллельный заданному вектору.

Рассмотрим прямую в плоскости XOY. Фиксировать прямую, параллельную данному вектору 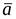с координатами 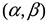мы сможем, задав одну точку с координатами 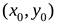, через которую прямая проходит. Выберем на прямой произвольную точку с координатами 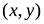. Тогда из подобия соответствующих треугольников имеем

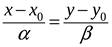. (1)

Вводя угловой коэффициент прямой 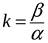(тангенс угла, образуемого прямой с положительным направлением 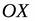), мы получим из (1) уравнение прямой с угловым коэффициентом: .

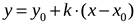Приравнивая нулю координаты направляющего вектора и 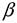, получим прямые, параллельные координатным осям: 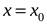и .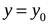

Прямая на плоскости может задаваться не только точкой и направляющим вектором, но и двумя различными точками.

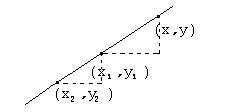
Составляя пропорции сторон подобных треугольников, получим соотношение 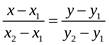. Это линейное соотношение представляет собой уравнение прямой, проходящей через две различные точки.