Производная обратной функции
Дана функция 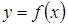 и обратная ей функция
и обратная ей функция 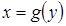 , т.е.
, т.е. 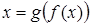 . Если
. Если 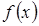 дифференцируема в точке x и
дифференцируема в точке x и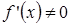 ,тогда
,тогда 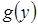 дифференцируема в точке
дифференцируема в точке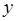 , при этом
, при этом 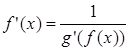 .
.
Действительно, т.к. 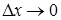 значит
значит 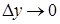 , о чем говорилось выше, причем оба приращения не равны нулю. Теперь
, о чем говорилось выше, причем оба приращения не равны нулю. Теперь
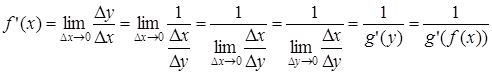 .
.
Пусть 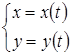 . Обе функции дифференцируемы. Вычислим
. Обе функции дифференцируемы. Вычислим
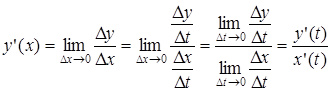 . Итак,
. Итак, 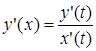 .
.
Таблица производных
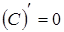 , если , если 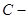 постоянная постоянная
| 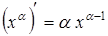
| 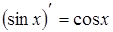
| 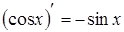
|
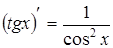
| 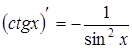
| 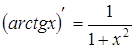
| 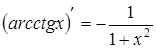
|
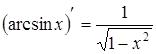
| 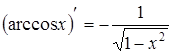
| 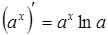
| 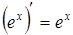
|
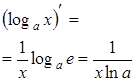
| 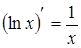
| 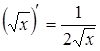
|
Докажем некоторые из этих формул.
· Если 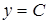 , то
, то 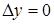 , и первая формула доказана.
, и первая формула доказана.
· Пусть 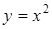 , тогда
, тогда
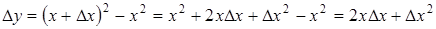 ,
,
откуда следует 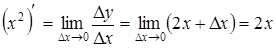 , то есть доказана вторая формула для
, то есть доказана вторая формула для 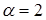 .
.
· Пусть 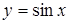 , тогда
, тогда 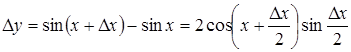 , ясно, что
, ясно, что
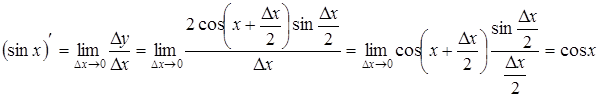 .
.
· Пусть 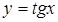 , тогда
, тогда 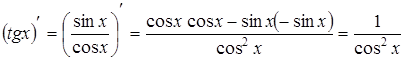
· Пусть 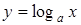 , тогда
, тогда
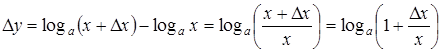 ,
,
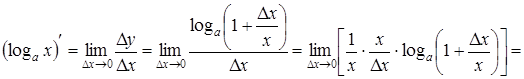
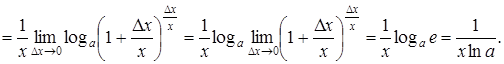
· Пусть 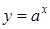 , тогда,
, тогда, 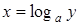 ,
, 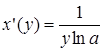 , значит
, значит
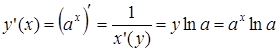 .
.
· Пусть 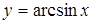 , тогда
, тогда 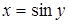 ,
, 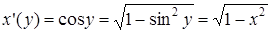 .
.
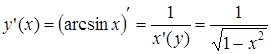 .
.
 2014-02-02
2014-02-02 324
324








