Терема Ролля. Пусть функция 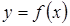 дифференцируема на интервале
дифференцируема на интервале 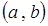 , причем
, причем 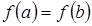 , тогда найдется хотя бы одна точка внутри интервала, в которой производная функции обращается в нуль, то есть
, тогда найдется хотя бы одна точка внутри интервала, в которой производная функции обращается в нуль, то есть 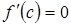 ,
, 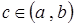 .
.
 Теорема дается без доказательства, ограничимся общими рассуждениями.
Теорема дается без доказательства, ограничимся общими рассуждениями.
Если 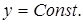 , то
, то 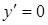 во всех точках интервала.
во всех точках интервала.
Пусть 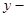 переменная и имеет одинаковые значения на границах интервала, тогда она обязательно принимает на рассматриваемом отрезке наибольшее и наименьшее значения, оба они не могут оказаться на границе отрезка (тогда они совпадают, что возможно только при
переменная и имеет одинаковые значения на границах интервала, тогда она обязательно принимает на рассматриваемом отрезке наибольшее и наименьшее значения, оба они не могут оказаться на границе отрезка (тогда они совпадают, что возможно только при 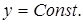 ). Пусть одно из них находится во внутренней точке интервала
). Пусть одно из них находится во внутренней точке интервала 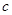 . Если это наибольшее значении, то при подходе к указанной точке функция возрастает, угол наклона касательной острый и тангенс этого угла положителен, после этой точки кривая убывает, угол наклона касательной тупой, его тангенс отрицателен. Производная, проходя точку
. Если это наибольшее значении, то при подходе к указанной точке функция возрастает, угол наклона касательной острый и тангенс этого угла положителен, после этой точки кривая убывает, угол наклона касательной тупой, его тангенс отрицателен. Производная, проходя точку 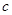 , меняет знак, и поскольку она существует, то не может в этой точке отличаться от нуля.
, меняет знак, и поскольку она существует, то не может в этой точке отличаться от нуля.
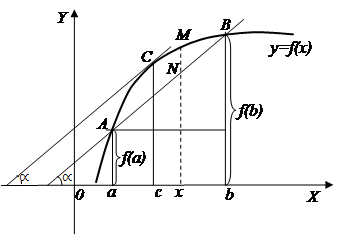 Теорема конечных приращений Лагранжа. Если функция
Теорема конечных приращений Лагранжа. Если функция 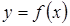 дифференцируема на интервале
дифференцируема на интервале 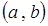 , то
, то
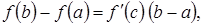 где
где 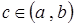 . (Без доказательства).
. (Без доказательства).
Теорема Коши. Если функции 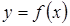 и
и 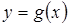 дифференцируемы на интервале
дифференцируемы на интервале 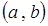 и
и 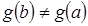 , то
, то 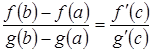
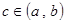 .
.
Доказательство. Рассмотрим вспомогательную функцию
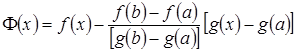 .
.
Она дифференцируема, так как кроме функций 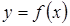 и
и 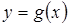 в нее входят только постоянные, причем,
в нее входят только постоянные, причем, 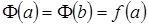 , то есть удовлетворяет всем условиям теоремы Ролля. Тогда
, то есть удовлетворяет всем условиям теоремы Ролля. Тогда 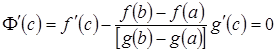 , теорема доказана.
, теорема доказана.
Замечание. При формулировке теоремы не следовало добавлять условие 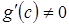 , так как оно следует из теоремы Лагранжа.
, так как оно следует из теоремы Лагранжа.
 2014-02-02
2014-02-02 300
300







