2014-02-02
261
Лекция 6
Определение 1. Функция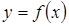 
называется дифференцируемой в точке x, если ее приращение 
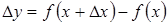представимо в виде 
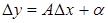, причем 
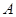не зависит от 
, 
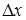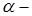бесконечно малая функция, более высокого порядка малости, чем 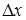, то есть 
.
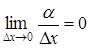Установим значение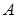 
, для чего вычислим
.
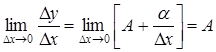Назовем число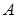производной функции 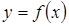в точке x и обозначим ее 
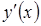, в результате получаем определение производной 
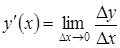и, кроме того,
.
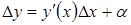Как было сказано выше, второе слагаемое в приращении функции более высокого порядка малости, чем 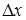, следовательно, и 
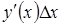. Другими словами, первое слагаемое представляет основную часть приращения функции. Называют его дифференциалом функции 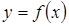и обозначают 
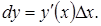В целях единообразия приращение аргумента 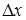в этой формуле обозначают 
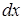. Тогда 
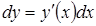, откуда следует второе обозначение производной 
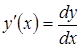. Связь между приращением функции, ее дифференциалом и 
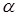изображена на рисунке.
Теорема. Дифференцируемая в некоторой точке функция непрерывна в ней. В самом деле, поскольку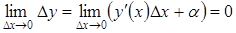 
, таким образом, из условия дифференцируемости функции имеем 
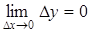, то есть условие ее непрерывности.
Если из условия непрерывности функции следует, что приращение функции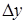 
бесконечно малая при 
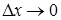, то из условия дифференцируемости получается, что 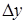бесконечно малая одного порядка малости с .
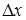Вычисление производной можем называть теперь дифференцированием функции.
