Вычисление производной на основе интерполяционного многочлена Лагранжа

Вычисление производной на основе интерполяционного многочлена Лагранжа применяется, когда аналитическое выражение функции y=f(x) не известно, а функция y=f(x) задана таблично.

Пусть функция y=f(x) определена на отрезке и в точках { x_i } (i=0,1,2,…,n) этого отрезка принимает значения y_i=f(x_i).

Разность между соседними значениями аргумента x_i постоянна и является шагом h=x_i – x_i-1 (i=1, …,n) разбиения отрезка на n частей, прием a=x₀ и b=x_n.

Найдем аппроксимации производной первого порядка с помощью значений функций y_i в узловых точках x_i.

Для того чтобы выразить значения производной через значения функции y_i в узлах интерполяции x_i, построим интерполяционный многочлен Лагранжа L_m(x) степени m, удовлетворяющий условиям

L_m(x)= f(x_k)= y_k (k=i, i+1, …, i+m), i+m£n

Многочлен Лагранжа L_m(x) интерполирует функцию f(x) на отрезке [ x_i, x_i+m ]. Дифференцируя многочлен L_m(x), получаем значения производной в точках { x_i } (k=i, i+1, …, i+m).

Если m=2, то график интерполяционного многочлена Лагранжа L₂(x) – парабола, проходящая через три точки (x_i, y_i), (x_i+1, y_i+1) и (x_i+2, y_i+2).

Вычислим первую производную многочлена L₂(x) на отрезке [ x_i, x_i+2 ]:

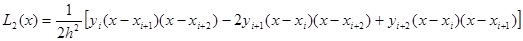
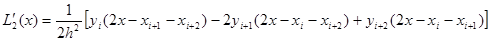
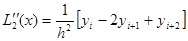
Производная многочлена L₂(x) в точках x_i, x_i+1, x_i+2 является приближением производной функции f(x) в этих точках:

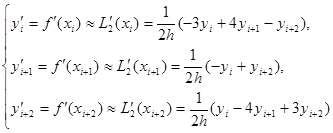(1)

Погрешности при вычислении производных в точках x_i, x_i+1, x_i+2 определяются следующим образом:

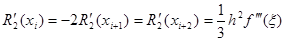(2)

Формулы (2) показывают, что погрешности аппроксимации первой производной 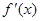с помощью формул (1) имеют один и тот же порядок O(h²), таким образом, можно вычислять производную на отрезке [a,b] в точках { x_i } (i=0,1,2,…,n) при n³2 по формулам:

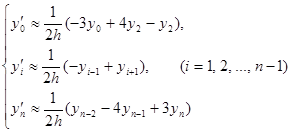(3)

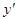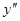Полагаем, что значения производных и в точках х, близких к точкам x_i, равны соответствующим значениям 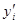и .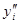

Будем считать точку близкой к x_i, если она принадлежит промежутку 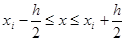. Точки х, близкие к точкам x_i, имеют одно и то же значение параметра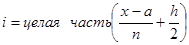

В зависимости от i при n³3 используем одну из формул (5).

Программа вычисления производной первого порядка на основе интерполяционного многочлена Лагранжа:

program deriveFunction1order;

const p=15;

type

vector = array [0..p] of real;

var i,n: integer;

a,b,h,x,y1: real;

y: vector;

BEGIN

repeat

writeln('Введите n - число разбиений отрезка [a,b]');

readln(n);

until (n>=3) and (n<=15);

writeln('Введите координаты концов отрезка [a,b]');

readln(a,b);

writeln('Введите значения функции y[i] в узлах,');

writeln('причем y0=f(a), yn=f(b)');

for i:=0 to n do readln(y[i]);

writeln('Введите x');

readln(x);

h:=(b-a)/n;

i:=trunc((x-a)/h+h/2);

if i=0 then y1:=(-3*y[0]+4*y[1]-y[2])/(2*h);

if (i>0) and (i<n) then y1:=(-y[i-1]+y[i+1])/(2*h);

if i=n then y1:=(y[n-2]-4*y[n-1]+3*y[n])/(2*h);

writeln('x=',x:6:3, 'производная 1 порядка=',y1:10:6);

readln

END.

Введите n - число разбиений отрезка [a,b]

Введите координаты концов отрезка [a,b]

2 3

Введите значения функции y[i] в узлах,

причем y0=f(a), yn=f(b)

4.00

6.71

10.08

14.17

19.04

24.75

31.36

38.93

47.52

57.19

68.00

Введите x

2.85

x = 2.850 производная 1 порядка = 91.300000