Определение скоростей и ускорений плоских рычажных механизмов методом планов
Данный метод позволяет вычислить величины скоростей и ускорений без использования аналитических зависимостей. Подробное изложение данного метода приведено в работах [1], [2]. Построение планов скоростей и ускорений выполним для кривошипно –ползунного механизма в положении, показанном на рис. 4.1.

Рис.4.1
Скорость точки А, принадлежащей звеньям 1 и 2, определим как окружную во вращательном движении: 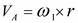 . Вектор
. Вектор 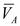 направлен перпендикулярно ОА в сторону
направлен перпендикулярно ОА в сторону 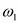 . Для определения скорости точки В, принадлежащей звеньям 2 и 3, разложим движение звена 2 на переносное поступательное вместе с точкой А и относительное вращательное вокруг точки А. Тогда имеем
. Для определения скорости точки В, принадлежащей звеньям 2 и 3, разложим движение звена 2 на переносное поступательное вместе с точкой А и относительное вращательное вокруг точки А. Тогда имеем 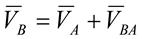 . (4.1)
. (4.1)
В данном уравнении вектор 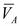 известен, линия действия
известен, линия действия 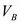 совпадает с линией движения ползуна, линия действия относительной скорости
совпадает с линией движения ползуна, линия действия относительной скорости 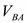 перпендикулярна линии АВ шатуна.
перпендикулярна линии АВ шатуна.
Решение этого векторного уравнения производим графически путем построения плана скоростей (рис.4.2).
Из полюса р проводим отрезок р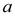 произвольной длины, изображающий вектор
произвольной длины, изображающий вектор 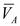 . Масштаб плана скоростей
. Масштаб плана скоростей 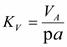 . Рекомендуется при построении принимать
. Рекомендуется при построении принимать 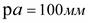 . Далее из полюса
. Далее из полюса  проводим линию действия скорости
проводим линию действия скорости 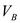 параллельно линии хода ползуна, а через точку
параллельно линии хода ползуна, а через точку 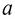 - линию действия
- линию действия 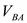 перпендикулярно АВ. Точка
перпендикулярно АВ. Точка 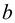 пересечения двух линий определяет величины векторов.
пересечения двух линий определяет величины векторов. 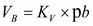 ;
; 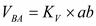 .
.
Направление векторов 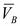 и
и 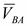 определяется по уравнению (4.1).
определяется по уравнению (4.1).
Угловая скорость шатуна 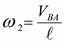 . Её направление определяется по направлению скорости
. Её направление определяется по направлению скорости 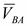 , приложенной в точке В.
, приложенной в точке В.
Для нахождения вектора скорости точки С шатуна воспользуемся изображающими свойствами плана скоростей [1]. В соответствии с ними три точки одного звена на схеме механизма и три соответствующие точки на плане скоростей образуют подобные и сходственно расположенные фигуры. В данном случае три точки А, В, С шатуна находятся на одной линии. Следовательно, изображающая точка С на плане скоростей будет расположена между точками 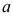 и
и  . Её положение определится из соотношения:
. Её положение определится из соотношения: 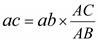 . Вектор
. Вектор 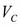 проводим из полюса
проводим из полюса  в точку С.
в точку С. 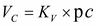 .
.
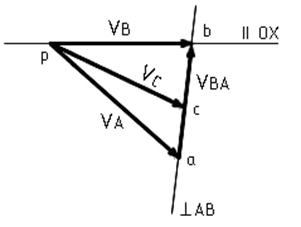 Рис.4.2
Рис.4.2
Построение плана ускорений выполним для того же положения механизма (рис.4.1).
Ускорение точки А складывается из двух составляющих: центростремительного и вращательного. 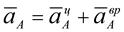 .
.
Для упрощения задачи будем считать угловую скорость кривошипа 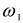 постоянной. Тогда угловое ускорение кривошипа
постоянной. Тогда угловое ускорение кривошипа 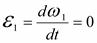 , и
, и 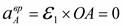 . Следовательно,
. Следовательно, 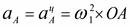 .
.
Вектор 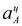 направлен параллельно ОА к центру вращения.
направлен параллельно ОА к центру вращения.
Определение ускорения точки В производится на основании разложения движения звена 2 на переносное поступательное с точкой А и относительное вращательное вокруг этой точки.
В соответствии с этим ускорение точки В определится из векторного уравнения 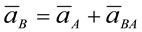
Так как относительное движение - вращательное: 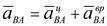 .
.
Тогда: 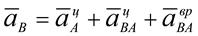 . (4.2)
. (4.2)
Следует заметить, что кориолисово ускорение в данном случае равно 0, так как переносное движение поступательное.
Центростремительное ускорение 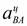 направлено параллельно шатуну от точки В к точке А.
направлено параллельно шатуну от точки В к точке А. 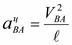 .
.
Вращательное ускорение 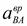 перпендикулярно
перпендикулярно 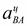 . Линия действия
. Линия действия 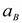 совпадает с линией движения ползуна. Решение уравнения (4.2) проводим графически путем построения плана ускорений (рис. 4.3).
совпадает с линией движения ползуна. Решение уравнения (4.2) проводим графически путем построения плана ускорений (рис. 4.3).
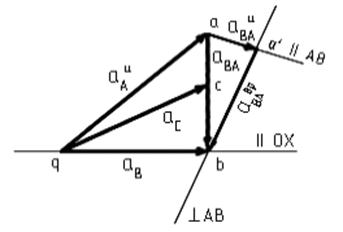
Рис.4.3
Из полюса 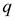 проводим отрезок
проводим отрезок 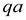 произвольной длины, изображающий вектор
произвольной длины, изображающий вектор 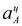 . Масштаб плана ускорений
. Масштаб плана ускорений 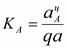 . Рекомендуется при построении принимать
. Рекомендуется при построении принимать 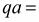 100мм. Далее, из точки
100мм. Далее, из точки 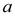 откладываем
откладываем 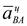 в виде отрезка
в виде отрезка 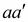 параллельно АВ в направлении от точки В к точке А.
параллельно АВ в направлении от точки В к точке А. 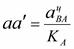
Из точки 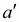 проводим линию действия
проводим линию действия 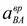 перпендикулярно шатуну АВ, а из полюса
перпендикулярно шатуну АВ, а из полюса 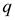 линию действия
линию действия 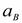 параллельно линии хода ползуна.
параллельно линии хода ползуна.
Точка 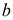 пересечения этих линий определяет величины ускорений.
пересечения этих линий определяет величины ускорений.
 ,
, 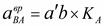 .
.
Направление векторов 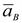 и
и 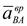 определяются по уравнению (4.2).
определяются по уравнению (4.2).
Угловое ускорение шатуна 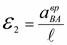 . Его направление определяется по направлению ускорения
. Его направление определяется по направлению ускорения 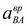 , приложенному в точке В.
, приложенному в точке В.
Для нахождения вектора ускорения точки С шатуна воспользуемся изображающими свойствами плана ускорений, которые аналогичны свойствам плана скоростей [2]. Изображающая точка С на плане ускорений будет находиться между точками 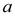 и
и 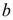 . Её положение определится из соотношения:
. Её положение определится из соотношения:
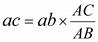 .
.
Вектор 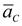 проводим из полюса
проводим из полюса 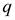 в точку С.
в точку С. 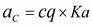 .
.
 2014-02-02
2014-02-02 3337
3337