Полный аналог относительного ускорения
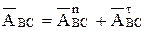
Аналог центростремительного (нормального) ускорения 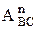 найдем по формуле
найдем по формуле
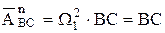
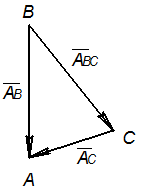 |
| Рис. 2.25 |
и примем равным отрезку ВС т.к. 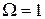
Аналог вращательного ускорения 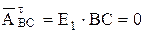 т.к.
т.к. 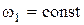 тогда
тогда
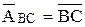
т.е. аналог относительного ускорения двух точек главного звена равен расстоянию между этими точками.
В то же время 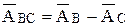 отсюда
отсюда
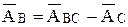
следовательно аналоги абсолютных ускорений точек В и С сходятся в т. А, которая называется полюсом поворота (рис. 2.25).
Если известен полюс поворота, то аналог ускорения любой точки находят как расстояние от этой точки до полюса поворота.
3.7. Построение полярных планов аналогов скоростей
Полярным планом скоростей механизма называется совокупность векторов линейных скоростей, отложенных из одной точки, называемой полюсом.
Рассмотрим построение полярного плана аналогов скоростей для кривошипно-ползунного механизма, (рис. 2.26).
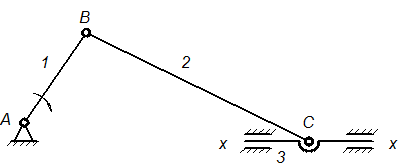 |
| Рис. 2.26 |
Из полюса Р – точки произвольно выбранной на чертеже, откладываем аналог скорости точки В. Направление этого вектора перпендикулярно кривошипу, длина его равна длине кривошипа.
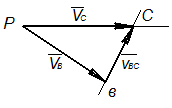
Для нахождения аналога скорости точки С напишем два векторных уравнения.
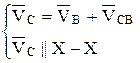
В этих уравнениях вектор 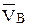 уже известен аналог относительной скорости точки С вокруг В следует направить перпендикулярно радиусу вращения ВС. Решив совместно эти два уравнения получаем на полярном плане аналог скорости точки С –
уже известен аналог относительной скорости точки С вокруг В следует направить перпендикулярно радиусу вращения ВС. Решив совместно эти два уравнения получаем на полярном плане аналог скорости точки С – 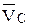 .
.
Решение этих уравнений производится в такой последовательности:
Из конца вектора 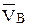 проводим прямую перпендикулярную отрезку ВС на механизме.
проводим прямую перпендикулярную отрезку ВС на механизме.
Из полюса Р проводим прямую параллельную направляющей х–х ползуна С.
Пересечение указанных прямых линий определяет конец аналога скорости точки С.
Отрезок, соединяющий буквы плана скоростей (вс) изображает аналог относительной скорости.
Величина скорости точек В и С:
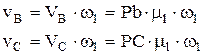
Итак, план скоростей является планом скоростей в масштабе
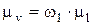
Рассмотрим построение полярного плана аналогов скоростей для кулисного механизма, (рис. 2.27).
Вектор аналога скорости 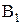 , принадлежащей кривошипу направлена перпендикулярно кривошипу. Из произвольного выбранного полюса Р откладываем этот вектор
, принадлежащей кривошипу направлена перпендикулярно кривошипу. Из произвольного выбранного полюса Р откладываем этот вектор 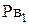 в размере равном длине кривошипа.
в размере равном длине кривошипа.
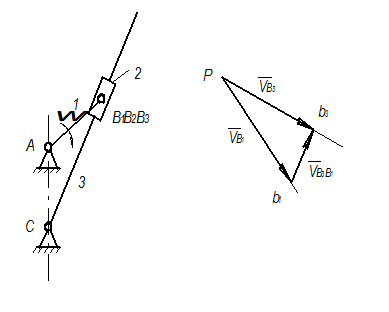
Рис. 2.27
Векторы аналогов скоростей точек 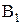 и
и 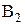 равны, т.к. объединены вращательной кинематической парой, т.е.
равны, т.к. объединены вращательной кинематической парой, т.е. 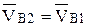 .
.
Для нахождения вектора скорости точки В3, принадлежащей кулисе, запишем систему векторных уравнений
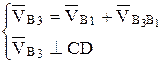
В этих уравнениях вектор 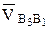 - это релятивная (относительная скорость) точки
- это релятивная (относительная скорость) точки 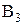 относительно
относительно 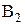 . Направлена эта скорость по кулисе, решив совместно эти два уравнения получаем точку "
. Направлена эта скорость по кулисе, решив совместно эти два уравнения получаем точку " 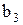 ",
", 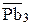 – вектор аналога скорости точки
– вектор аналога скорости точки 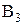 .
.
Аналог скорости точки D найдется из пропорции
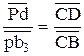
Аналог угловой скорости кулисы 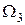 найдем из выражения, тогда
найдем из выражения, тогда 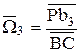
Угловая скорость кулисы определится по формулам
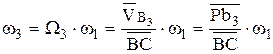
Истинная скорость точек механизма найдем через аналог скоростей, как 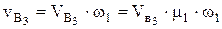 и т.д.
и т.д.
3.8. Построение планов аналогов скоростей методом эпюр
Рассмотрим определение скоростей подобным методом в четырехзвеннике ABCDE, (рис. 2.28).
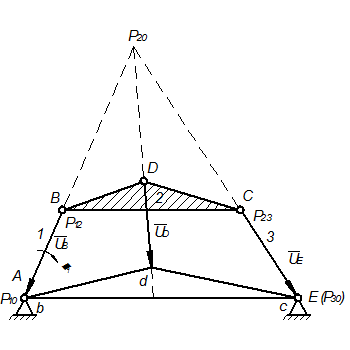
Рис. 2.28
На схеме механизма, вычерченной в масштабе 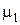 , отмечаем МЦОВ (
, отмечаем МЦОВ (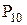 ,
, 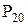 ,
, 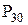 ). Затем откладываем вектор аналога повернутой скорости точки В первого звена так, чтобы
). Затем откладываем вектор аналога повернутой скорости точки В первого звена так, чтобы 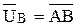 . Аналог скорости точки В первого звена равен аналогу скорости точки В второго звена, имея вектор
. Аналог скорости точки В первого звена равен аналогу скорости точки В второго звена, имея вектор 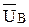 переходим к нахождению аналога скорости точки С второго звена. Направление повернутой скорости
переходим к нахождению аналога скорости точки С второго звена. Направление повернутой скорости 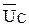 совпадает с линией, соединяющей точку С с МЦОВ (
совпадает с линией, соединяющей точку С с МЦОВ (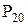 ) этого звена. Начало вектора в самой точке С, конец на эпюре
) этого звена. Начало вектора в самой точке С, конец на эпюре 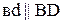 .
.
Вектор аналога повернутой скорости точки D совпадает по направлению с линией, соединяющей эту точку с 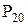 . Начало вектора лежит в точке D, конец на эпюре
. Начало вектора лежит в точке D, конец на эпюре 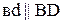 .
.
Итак 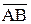 - изображение аналога скорости
- изображение аналога скорости 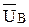
Скорость точек В, С, и D определяется как
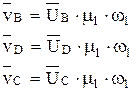
Аналог угловой скорости найдем из выражения
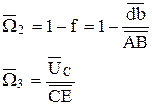
Рассмотрим пример построения плана аналогов скоростей методом эпюр для кулисного механизма, (рис. 2.29)
Кривошип АВ совершает вращательное движение вокруг неподвижной оси А.
Кулиса 3 совершает колебательное движение вокруг центра С.
Наносим МЦВ всех звеньев (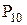
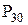 ). Точка
). Точка 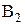 ползуна совершает вращательное движение вместе с точкой кривошипа
ползуна совершает вращательное движение вместе с точкой кривошипа 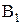 поэтому
поэтому 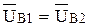 .
.
Направление аналога повернутой скорости точек 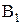 и
и 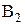 совпадает с направлением кривошипа, начало вектора – в точке В, конец – в МЦОВ –
совпадает с направлением кривошипа, начало вектора – в точке В, конец – в МЦОВ – 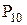 .
.
Скорость точек 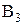 и
и 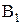 разные, т.к. траектории их разные.
разные, т.к. траектории их разные.
Точка 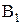 перемещается по траектории
перемещается по траектории 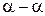 , точка
, точка  – по траектории
– по траектории 
Эти скорости связаны следующим соотношением:
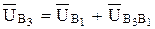
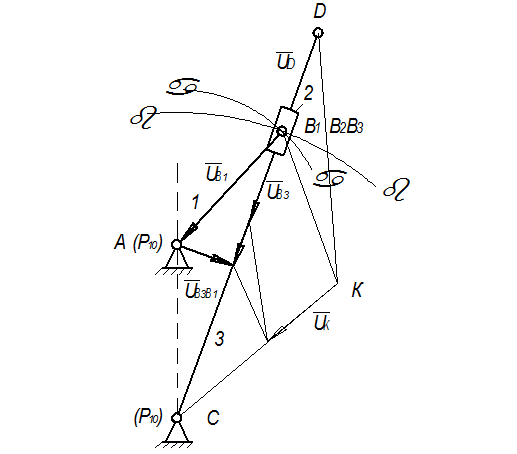
Рис. 2.29
Где 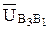 - вектор относительной повернутого аналога скорости точек
- вектор относительной повернутого аналога скорости точек 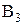 относительно
относительно 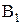 на плане этот вектор необходимо направить перпендикулярно направляющей кулисы.
на плане этот вектор необходимо направить перпендикулярно направляющей кулисы.
И в то же время абсолютная скорость точки 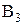 , вращающейся вокруг неподвижного центра
, вращающейся вокруг неподвижного центра 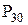 , направлена
, направлена 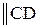 , т.е. радиусу вращения.
, т.е. радиусу вращения.
Тогда аналог повернутой скорости
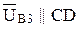
Решая совместно эти два уравнения, находим конец вектора 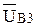 .
.
Аналог повернутой скорость точки D находим с помощью вспомогательной точки К, произвольно отмеченной и принадлежащей звену 3. Вектор повернутой скорости этой точки направлен по линии проходящей через МЦОВ звена 3 и саму точку К. Начало вектора – в точке К,
конец – на эпюре 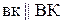 . Далее соединим точку К с точкой D. Вектор аналога повернутой скорости точки D направлен по звену 3, начало – в точке D, конец на эпюре
. Далее соединим точку К с точкой D. Вектор аналога повернутой скорости точки D направлен по звену 3, начало – в точке D, конец на эпюре  .
.
Таким же способом можно найти вектор повернутой скорости центра тяжести звена 3.
Скорость точек определяют как
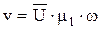
Аналог угловых скоростей определяем
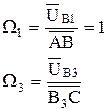
 2015-01-22
2015-01-22 1126
1126








