Устойчивость явной разностной схемы (11), (8)

Обозначим 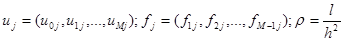. Введем нормы .

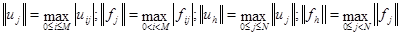Теорема 1. Если 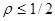, то разностная схема (11), (8) устойчива.

Доказательство. Перепишем (11) в виде . Если 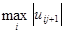достигается во внутреннем узле 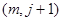, то 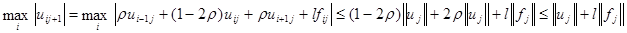. В противном случае .

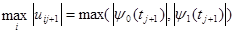Таким образом, получается оценка

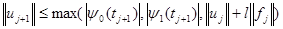. (12)

Представим решение 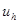разностной схемы (11), (8) в виде , где 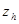- решение задачи (11), (8), когд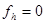а , а 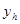- решение задачи (11), (8) при однородных начальных и граничных условиях. Применяя оценку (12) для 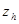, получаем

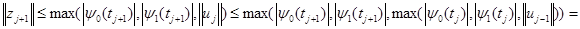
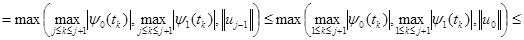
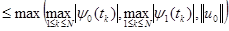
Для 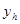применение оценки (12) дает

.

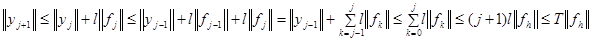В результате имеем 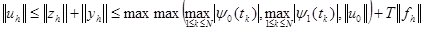. Теорема доказана.

Явная разностная схема (11), (8) является условно устойчивой.