2014-02-02
348
Рассмотрим задачу
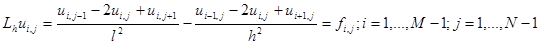,(8)
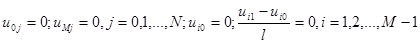. (9)
Решение разностной задачи (8), (9) будем искать в виде
. (10)
где 
как функция j при фиксированном p удовлетворяет однородному разностному уравнению
, (11)
однородным краевым условиям
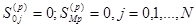(12)
и начальным условиям
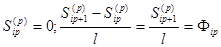. (13)
Векторы 
выберем так, чтобы удовлетворялось неоднородное уравнение (8).
Из определения следует,что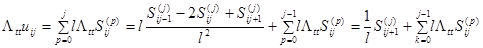 
, 
.
Подстановка последних выражений в (8) дает
; 
,
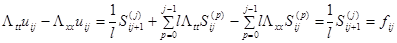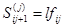откуда получаем 
. Остальные значения можно положить равными нулю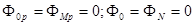 
.
Для решения задачи (11), (12), (13) можно воспользоваться оценкой из п.11.8: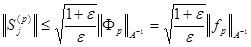 
. Оценка решения задачи (8) - (10) при этом примет вид 
.
В общем случае разностной схемы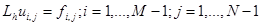 
при начальных условиях 
; 
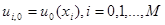и однородных граничных условиях 
приходим к оценке
.
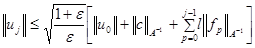При изложении материала за основу взяты страницы 313-315 учебного пособия: Самарский А.А. Теория разностных схем.-М.:Наука,1983.
