Устойчивость разностной схемы по начальным условиям

17 18 19 20 21 22 23

Рассмотрим разностную схему с однородным главным сеточным уравнением

, (8)

неоднородными начальными условиями

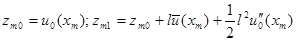(9)

и однородными граничными условиями

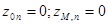. (10)

Уравнения (8) перепишем в кратком виде

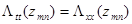(8 ’)

Будем искать частные нетривиальные решения уравнения (8’) в виде . Подставляя это выражение в (8’), имеем 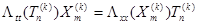. Отсюда получаем 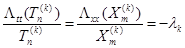, (11)

где 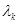- некоторое число. Учитывая однородные граничные условия (10), приходим к следующей задаче на собственные значения для оператора :

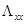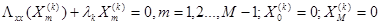(12)

Разностное уравнение (12) легко преобразуется к виду

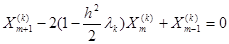. (13)

Общее решение разностного уравнения (13) имеет вид ,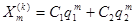

где 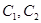- произвольные константы; 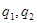- корни характеристического уравнения 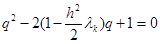. Корни характеристического уравнения определяются формулой 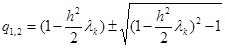, а множители 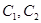определяются из граничных условий: 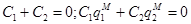. Отсюда получаем, что для существования нетривиального решения необходимо, чтобы 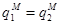. Учитывая, что , получаем 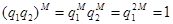. Отсюда, представляя 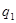в тригонометрической форме , имеем 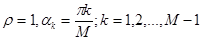. Из выражения для корней характеристического уравнения найдем : ;

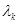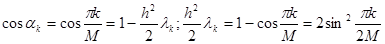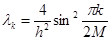. Для собственных значений 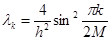собственные векторы определены с точностью до произвольного множителя 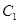. Взяв 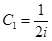, получим .

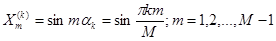Докажем, что собственные векторы 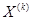с компонентами 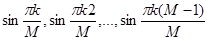образуют ортогональную систему со скалярным произведением 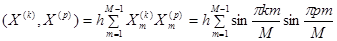. Имеем

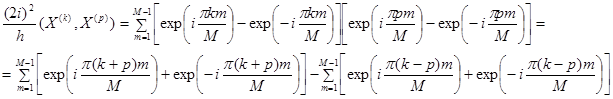
Обозначим . Суммируем

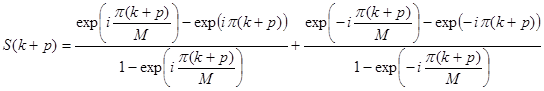
Очевидно, когда 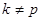, то

и получаем , ч.т.д.

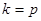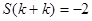
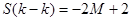Проведем теперь нормировку системы векторов. Когда , то и .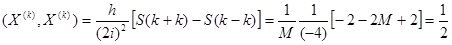

В дальнейшем будем использовать ортонормированную систему векторов 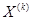с компонентами .

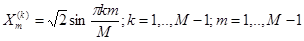Систему векторов 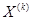можно взять в качестве координатной в (M-1)-мерном пространстве векторов и раскладывать по ней все другие вектора. Так для вектора a с компонентами 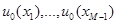в дальнейшем будем использовать разложение , где коэффициенты могут быть вычислены по формуле 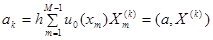. Отметим, что 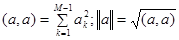. Для вектора 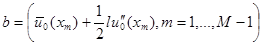будет использоваться разложение 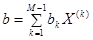с коэффициентами .

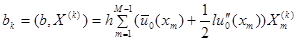Перейдем к решению задачи для 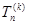: 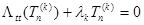или в развернутом виде

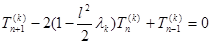. (14)

Так как 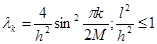, то 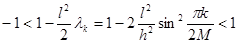. Поэтому характеристическое уравнение 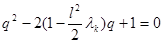имеет равные по модулю единице комплексно сопряженные корни .

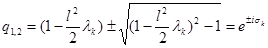Таким образом, общее решение уравнения (14) можно записать в виде

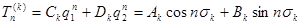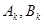, где - произвольные постоянные

Будем искать решение задачи (8) - (10) в форме

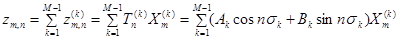. (15)

Сеточная функция (15) при произвольных наборах констант 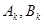удовлетворяет сеточному уравнению (8) и однородным граничным условиям (10). Распорядимся выбором констант 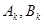так, чтобы удовлетворялись начальные условия (9). На нулевом слое (n=0) должно выполняться начальное условие 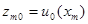, то есть 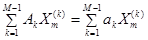. Так как векторы 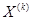линейно независимы, отсюда получаем .

Использование второго начального условия из (9) 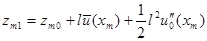дает относительно искомых коэффициентов 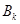уравнения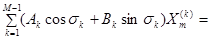 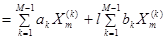. Отсюда находим 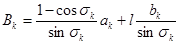. Подставим выражения для 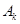и 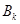в (15):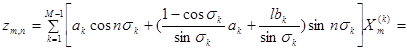

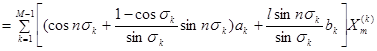. Учтем, что

. Тогда получим

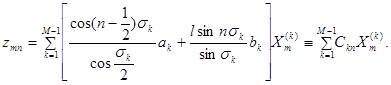(16)

Оценим 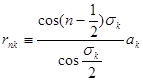и 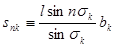. Имеем .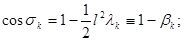

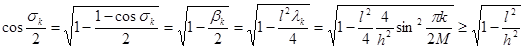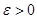В дальнейшем будем считать, что условие Куранта выполняется строго: , где - произвольное положительное число. Отсюда получаем первую оценку

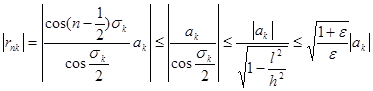. (17)

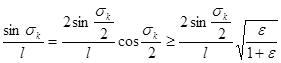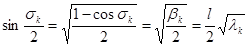Так как и , то

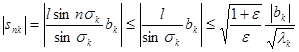. (18)

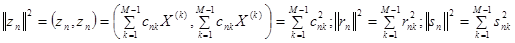
Применяя к сумме векторов аксиому треугольника для норм, получим

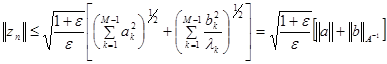. (19)

Здесь для правой части второго начального условия использована негативная норма

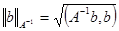, где A – матрица системы 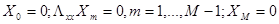. Собственные значения 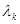и собственные векторы 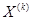, найденные выше для оператора , очевидно, являются таковыми и для матрицы A. Поэтому