Замечание 5

2.

1.

;

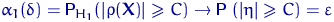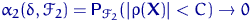для любого распределения 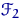, отвечающего .

Иначе говоря, построенный критерий имеет асимптотический размер 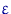и состоятелен.

5.1. Критерии согласия: критерий 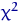Пирсона

Критерий 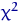(K.Pearson, 1903) основывается на группированных данных. Область значений предполагаемого распределения 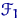делят на некоторое число интервалов. После чего строят функцию отклонения по разностям теоретических вероятностей попадания в интервалы группировки и эмпирических частот.

Имеется выборка 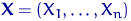из распределения 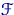. Проверяется простая гипотеза 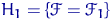против сложной альтернативы .

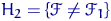Пусть 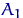, , 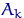— интервалы группировки в области значений случайной величины с распределением 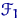. Обозначим для 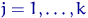через 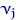число элементов выборки, попавших в интервал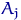

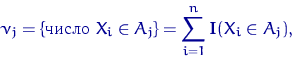
и через — теоретическую вероятность 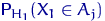попадания в интервал 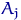случайной величины с распределением 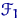. С необходимостью, . Как правило, длины интервалов выбирают так, чтобы .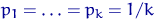

Пусть

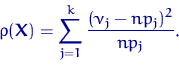
(4)

Свойство K1(б) выполнено далеко не для всех альтернатив. Если распределение выборки 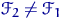имеет такие же, как у 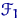, вероятности 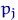попадания в каждый из интервалов 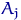, то по данной функции 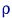эти распределения различить невозможно.

Поэтому на самом деле критерий, который мы построим по функции 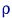из (4), решает совсем иную задачу. А именно, пусть задан набор вероятностей 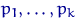такой, что . Критерий 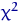предназначен для проверки сложной гипотезы

против сложной альтернативы 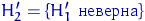, т.е.

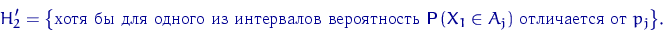
Покажем, что удовлетворяет условию K1(a).

Теорема 3 (Пирсона).

Если верна гипотеза , то при фиксированном и при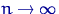

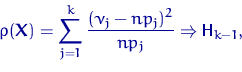
где, напомним, 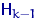есть 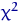-распределение с 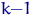степенью свободы.