Замечание 6

Сходимость по распределению обеспечивается ЦПТ, поэтому разница допредельной и предельной вероятностей имеет тот же порядок, что и погрешность нормального приближения

(см. неравенство Берри — Эссеена для погрешности в ЦПТ), где 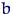— некоторая постоянная. Маленькие значения 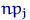в знаменателе приведут к тому, что распределение 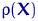будет существенно отличаться от 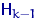. Тогда и реальная вероятность — точный размер полученного критерия — будет сильно отличаться от 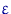. Поэтому для выборки объема 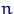число интервалов разбиения выбирают так, чтобы обеспечить нужную точность при замене распределения 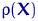на .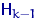

Обычно требуют, чтобы 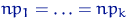были не менее -.

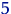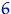5.2. Проверка гипотезы независимости: критерий хи-квадрат Пирсона

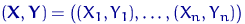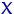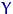Есть выборка значений двух наблюдаемых совместно случайных величин и в 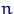независимых экспериментах. Проверяется гипотеза .

Введем 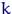интервалов группировки 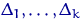для значени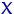й и интервалов группировки 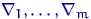для значений .

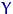Посчитаем эмпирические частоты:

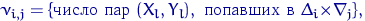
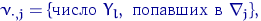
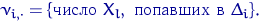
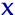
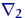
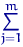
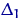
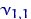
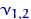
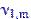
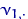
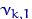
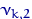
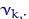
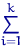
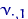
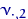
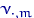
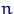
Если гипотеза верна, то теоретические вероятности попадания пары 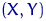в любую из областей 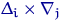равны произведению вероятностей: для всех 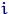и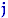

.

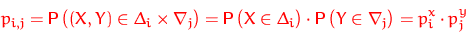Именно эту гипотезу (назовем ее ) мы в действительности и проверяем.

По ЗБЧ

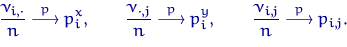
Поэтому значительная разница между 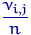и 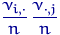(или между 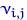и 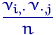) может служить основанием для отклонения гипотезы независимости.

Пусть

(5)