2014-02-02
327
K2.
K1.
Пусть возможно задать функцию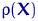 
, обладающую свойствами:
а) если гипотеза 
верна, то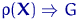 
, где 
— непрерывное распределение;
б) если гипотеза неверна, то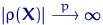 
при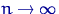 
.
Пусть такая функция 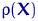задана. Для случайной величины 
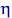из распределения определим постоянную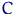 
из равенства 
.
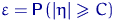Построим критерий:
| (3) |
Мы построили критерий согласия. Он «работает» по принципу: если для данной выборки функция отклонения велика (по абсолютному значению), то это свидетельствует в пользу альтернативы, и наоборот. Убедимся в том, что этот критерий имеет (асимптотический) размер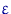 
и является состоятельным.
Говорят, что критерий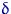 
для проверки простой гипотезы является критерием асимптотического размера 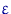, если его размер приближается к 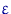с ростом 
:
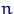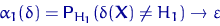при .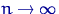
Поскольку альтернатива 
всегда является сложной, то, как мы уже отмечали в замечании 4, вероятность ошибки второго рода любого критерия 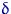есть функция 
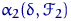от конкретного распределения 
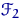из списка возможных альтернатив 
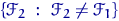. Или, при ином виде основной гипотезы, из числа распределений, отвечающих альтернативе .
