Метод максимального правдоподобия. Оценки неизвестных параметров находят с помощью метода максимального правдоподобия

Оценки неизвестных параметров находят с помощью метода максимального правдоподобия. Он предписывает выбирать неизвестные параметры так, чтобы максимизировать функцию правдоподобия случайного вектора .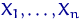

Будем, для простоты, предполагать, что вектор ошибок 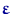состоит из независимых и одинаково распределенных случайных величин с плотностью распределения 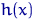из некоторого семейства распределений с нулевым средним и, вообще говоря, неизвестной дисперсией. Очень часто полагают, что 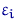имеют симметричное распределение — нормальное 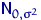, Стьюдента, Лапласа, логистическое и т.п. Поскольку 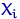от 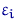зависят линейно, то распределение 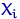окажется таким же, как у 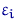, но с центром уже не в нуле, а в точке 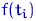. Поэтому 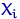имеет плотность 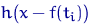, и функция правдоподобия вектора 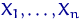равна, в силу независимости координат,

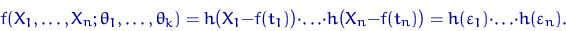
(7)

Если величины 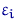имеют разные распределения, то 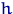следует заменить на соответствующие 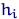. В отсутствие независимости произведение плотностей в (7) заменится плотностью совместного распределения координат вектора .

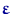Метод максимального правдоподобия предписывает находить оценки неизвестных параметров 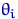функции 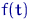и оценки неизвестной дисперсии (или дисперсий) 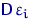, максимизируя по этим параметрам функцию правдоподобия (7). Рассмотрим, во что превращается метод максимального правдоподобия в наиболее частых на практике предположениях.