Поле направлений и приближённое построение интегральных кривых

Рассмотрим уравнение в нормальной форме

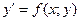. (1)

Пусть функция определена на некотором множестве 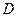изменения переменных 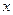и 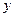. Тогда в каждой точке этого множества уравнение (1) определяет значение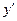, т.е. угловой коэффициент касательной к интегральной кривой в этой точке. Если в каждой точке множества 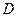задано значение некоторой величины, то говорят, что на этом множестве задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений. Получить наглядное представление о поле направлений уравнения (1) можно с помощью следующего процесса. Выберем некоторую точку множества 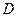, пусть её координаты есть 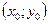. Построим отрезок с центром в этой точке так, чтобы угол 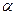наклона этого отрезка к положительному направлению оси удовлетворял условию

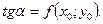(2)

Если проделать такое построение для достаточно большого количества точек множества 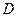, то получим сеть отрезков, для каждого из которых тангенс угла его наклона к оси совпадает со значением функции в центральной точке отрезка. Построенная сеть отрезков и есть поле направлений уравнения (1).

Проведём теперь на той же плоскости интегральную кривую уравнения (1). Пусть это будет график некоторого решения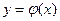. Тогда выполняется тождество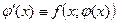, следовательно, в точке 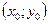получим: 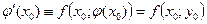. Вспомним, что с геометрической точки зрения производная функции в некоторой точке – это тангенс угла наклона касательной к кривой, являющейся графиком данной функции, в этой точке.

Тогда уравнение (1) выражает геометрически тот факт, что направление касательной в каждой точке интегральной кривой совпадает с направлением поля уравнения (1) в этой точке. Это свойство отличает интегральные кривые уравнения (1) от кривых, не являющихся для него интегральными.

Приближённо построить интегральные кривые уравнения (1) на плоскости можно с помощью свойств функции , а также изоклин.

Изоклиной уравнения (1) называется линия, задаваемая уравнением

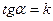, (3)

где 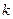- некоторая постоянная. Очевидно, что в каждой точке такой линии направление поля уравнения (1) одинаково. Угол наклона поля на фиксированной изоклине находится из условия

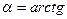
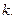(4)

Придавая числу 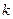различные значения, определяем по формуле (4) угол наклона поля на соответствующих изоклинах.

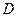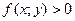Предположим, что на некоторых подмножествах множества функциясохраняет знак. Если на множестве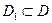, то и 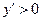на множестве , тогда все интегральные кривые уравнения (1) на множестве направлены снизу вверх, т.е. решения уравнения возрастают. Аналогично, если 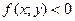на множестве 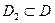, то и на множестве 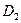, тогда все интегральные кривые уравнения (1) на множестве 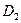направлены сверху вниз, значит, на этом подмножестве решения уравнения убывают.

Определим возможное геометрическое место точек экстремумов решений уравнения (1). Пусть 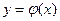- решение уравнения, тогда в точке экстремума необходимо выполняется 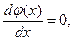откуда следует, что в этой точке 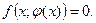Это значит, что экстремумы решений (если они существуют) могут лежать только на линии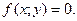Эта линия, очевидно, является изоклиной и называется изоклиной нуля.

Выясним теперь, чем отличается геометрическое место точек минимума интегральных кривых уравнения (1) от геометрического места точек их максимума. Вспомним, что в точках минимума кривой 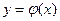выполняются условия и 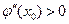, а в точках максимума этой кривой – условия и 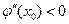. Вычислим тогда величину

.

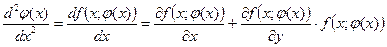В точках экстремума будет иметь место равенство 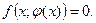Тогда в этих точках

.

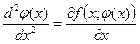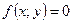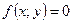Итак, геометрическое место точек минимума интегральных кривых уравнения (1) задаётся условиямии , а геометрическое место точек максимума – условиямии 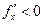. Если же 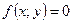и 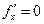- то получается геометрическое место точек перегиба интегральных кривых уравнения (1).

Исследование второй производной помогает определить подмножества множества 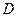, на которых интегральные кривые выпуклы вверх или вниз. Так, если функция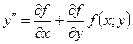положительна на некотором подмножестве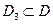, то на нём интегральные кривые выпуклы вниз; если же эта функция отрицательна – то они выпуклы вверх.

Предположим далее, что функция на некоторых линиях принимает бесконечные значения. На таких линиях поле направлено вертикально. Чтобы не исключать эти линии из рассмотрения, используем уравнение

.

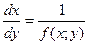Может оказаться, что в некоторых точках множества 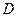функция принимает вид не раскрываемой неопределённости вида 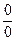. В таких точках поле направления уравнения (1) не определено, не определено в них и само уравнение. Через такие точки интегральные кривые уравнения (1) не могут проходить, однако могут существовать интегральные кривые, неограниченно приближающиеся (примыкающие) к таким точкам.

Используя всю полученную информацию, можно приближённо провести интегральные кривые уравнения (1) на плоскости.

Пример 1. Приближённо построить интегральные кривые уравнения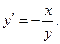

Поле направлений уравнения определено на всей плоскости 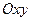, за исключением начала координат, где имеет место неопределённость вида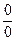. Для точек оси 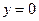следует рассмотреть перевёрнутое уравнение 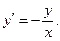Во всех точках оси 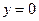направление поля параллельно оси . Интегральные кривые возрастают, когда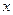и 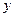имеют разные знаки и убывают в противоположном случае. Изоклина нуля имеет вид 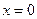. Для установления характера экстремумов определим величину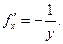Отсюда вытекает, что максимумы интегральных кривых расположены выше оси 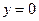, а минимумы – ниже этой оси. Величина 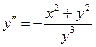, значит, выше оси 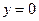интегральные кривые выпуклы вверх, а ниже этой оси – выпуклы вниз. Построим семейство изоклин. Оно будет иметь вид 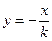, следовательно, на прямой 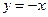угол наклона поля равен 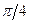, а на прямой 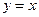он равен 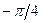. Можно заметить также, что с возрастанием 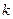угол наклона поля увеличивается, а с убыванием 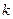- уменьшается. Теперь можно построить семейство интегральных кривых.