Теорема о существовании решения (теорема Пеано)

Задача Коши. Общее, частное и особое решения

Снова рассмотрим уравнение в нормальной форме

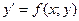. (1)

Будем считать, что функция определена на некотором множестве 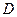изменения переменных 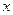и 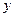. Рассмотрим некоторую точку 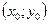этого множества и поставим задачу: найти решение уравнения (1), удовлетворяющее условию

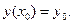(2)

Геометрически это означает, что требуется найти интегральную кривую уравнения (1), проходящую через заранее заданную точку 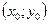множества .

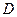Определение 1. Числа 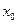и 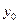называются начальными данными, условие (2) называется начальным условием, а задача нахождения решения уравнения (1), удовлетворяющего условию (2) называется задачей Коши.

Далее нам предстоит ответить на вопросы, при каких условиях решение задачи Коши существует? При каких условиях такое решение является единственным? Что называется единственностью? В каком случае через каждую точку множества проходит одно и только одно решение?

Определим сначала понятия точки единственности и точки не единственности.

Определение 2. Будем говорить, что через точку 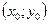проходит единственное решение уравнения (1), если для любых двух решени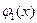й и 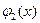этого уравнения, удовлетворяющих условию 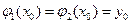, существует число 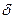, такое что на интервале 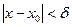выполняется тождество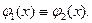

Точка 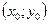называется при этом точкой единственности, а в случае нарушения этого определения – точкой не единственности.

Приведём теперь формулировки теорем, дающих ответы на поставленные вопросы.

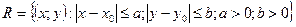Пусть функция задана на множествеи непрерывна на этом множестве по 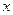и 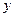. Тогда существует по крайней мере одно решение уравнения (1), удовлетворяющее условию (2), и это решение определено по крайней мере на отрезк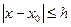е , где 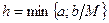, причём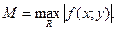

Теорема о существовании и единственности решения (теорема Пикара).

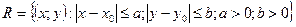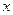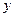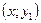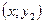Пусть функция задана на множествеи непрерывна на этом множестве по и . Пусть для любых двух точек и множества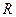выполнено условие Липшица по аргументу:

.

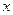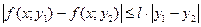Тогда решение уравнения (1), удовлетворяющее условию (2), существует и единственно; оно определено по крайней мере на отрезк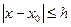е , где 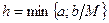, причём 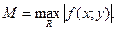Константа 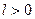называется константой Липшица.

Доказательства этих теорем будут приведены в следующих параграфах.

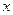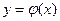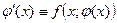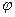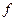В дальнейшем будем всегда предполагать, что– непрерывная функция своих аргументов. При этом всякое решение уравнения (1) будет непрерывно-дифференцируемой функцией аргумента . Действительно, пусть - решение уравнения (1), тогда выполняется тождество . Поскольку и - непрерывные функции своих аргументов, правая часть тождества – непрерывная функция 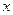, следовательно, решение 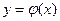имеет непрерывную первую производную.

Дадим теперь определение общего решения уравнения (1).

Определение 3. Общим решением уравнения (1) на множестве 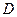называется однопараметрическое семейство функций

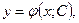(3)

таких что выполняются следующие условия:

1) каждая функция семейства (3) непрерывно-дифференцируема по аргументу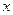 на некотором интервале;

2) для любой точки 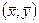множества 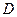соотношение (3) разрешимо относительно произвольной константы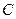

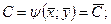(4)

3) для всякого значения константы 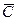, определяемого формулой (4), если точка 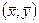берётся из множества 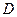, функция 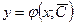является решением уравнения (1).

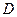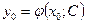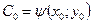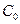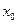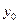Если известно общее решение уравнения (1) на множестве и условие (2), то решение задачи Коши (1)-(2) можно получить следующим образом. Подставим начальное условие в формулу (3), тогда . Выразим отсюда величину , получив таким образом её числовое значение. Теперь подставим это значение опять в формулу (3) и получим искомое решение задачи Коши. Учитывая зависимость значения от начальных данных и , это решение можно записать ещё и так

(5)

Замечание 1. Если в формуле (2) зафиксирована только величина 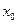, а величина 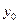– произвольна, т.е. равенство (2) рассматривается не как условие, а как обозначение, то формула (5) определяет общее решение уравнения (1) в форме Коши, где 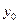– обозначение произвольной постоянной.

Если общее решение уравнения (1) записанов виде (3), то говорят, что оно задано в явном виде. Общее решение может быть записано также в неявном виде.

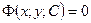или .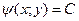

Эта форма записи называется общим интегралом уравнения (1) на множестве .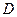

Кроме этого, общее решение может быть задано и в параметрической форме, т.е. в виде пары соотношени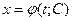й и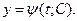

Определение 4. Решение уравнения (1) называется частным решением, если каждая его точка является точкой единственности; всякое частное решение уравнения входит в его общее решение при некотором значении произвольной константы 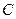, конечном или бесконечном.

Определение 5. Решение уравнения (1) называется особым решением, если каждая его точка является точкой не единственности; особое решение уравнения не входит в его общее решение ни при каком значении произвольной константы.

Замечание 2. Уравнение (1) может также иметь решения, представляющие собой гладкую склейку частного и особого решений. Такие решения не относятся ни к частным, ни к особым.

Пример 1. В уравнении 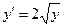частное решение, проходящее через точку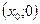, задаётся формулой 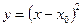, 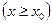. Через эту же точку проходит и особое решение 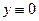. В качестве указанной склейки можно рассмотреть решение, задаваемое следующим образом:

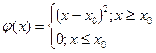
Если для уравнения (1) на некотором множестве 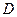выполнена теорема Пикара, то через каждую внутреннюю точку этого множества проходит одно и только одно решение уравнения (1). Действительно, вокруг каждой внутренней точки множества 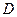, как вокруг центральной, может быть построено множество 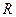с параметрам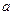и и 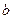выбранными так, чтобы 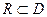. Тогда по теореме Пикара через эту точку множества будет проходить ровно одно решение уравнения (1). Таким образом при выполнении теоремы Пикара на некотором множестве уравнение (1) не будет иметь особых решений на этом множестве.