Критерий Гурвица. САУ будет устойчива, если при a0>0 все определители матрицы Гурвица будут положительны

САУ будет устойчива, если при a₀>0 все определители матрицы Гурвица будут положительны.

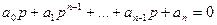
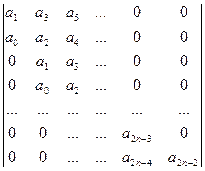
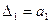
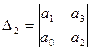
Частные случаи критерия Гурвица.

n=1,2,3,4

1. n=1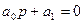

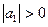
При n=1 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

2. n=2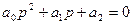

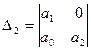
1).

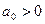
2).

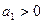
3).

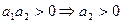
Необходимое и достаточное условие аналогично n=1.

3. n=3

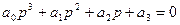
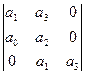
1).

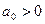
2).

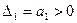
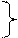3).

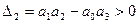
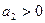
4).

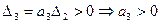
При n=3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов (а₁, а₂)было больше произведения крайних (а₀, а₃).

4. n=4

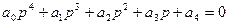
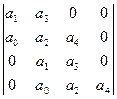
1).

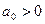
2).

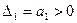
3).

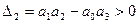
4).

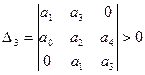
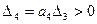
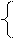При n=4 система будет устойчива при всех коэффициентах больших нуля и при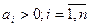

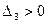
Критерий Гурвица удобно использовать при n<5. При n>5 критерий Гурвица становится громоздким и применяют критерий Рауса.