Устойчивость САУ.
Передаточная функция типовой схемы.
Пример.
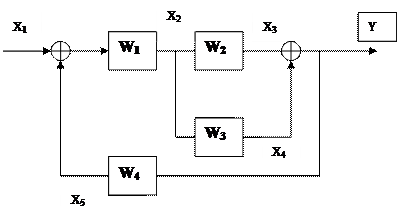 |
Сигнальный граф соответствующий данной САУ будет выглядеть так:
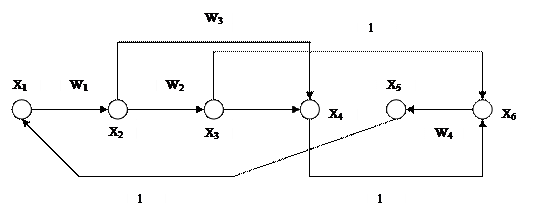 |
 |
Передаточная функция по задающему воздействию:
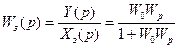
Передаточная функция по возмущающему воздействию:
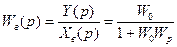
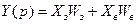
 | |||||
 | |||||
 | |||||
Нейтральное состояние
Нестойчивое состояние Устойчивое состояние
Устойчивым равновесным состоянием называется состояние, в которое возвращается объект после снятия внешней силы, выведшей его из этого состояния. Аналогично для движения САУ можно дать следующее определение: движение САУ называется устойчивым, если по истечению определенного времени система возвращается в это движение после снятия внешнего воздействия, выведшего данную САУ из данного движения.
Динамика процесса может быть представлена следующим уравнением
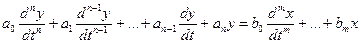 (1)
(1)
Анализ этого уравнения показал, что на устойчивость САУ влияет свободная составляющая.


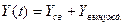
Общее решение Частное решение
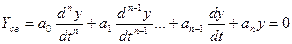 (2)
(2)
При 
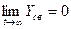 САУ находится в устойчивом состоянии.
САУ находится в устойчивом состоянии.
При 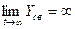 САУ находится в неустойчивом состоянии.
САУ находится в неустойчивом состоянии.
В любом другом случае САУ находится на границе устойчивости.
Уравнение (2) перепишем в операторном виде:
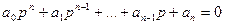 (3)
(3)
Решения алгебраического уравнения 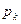 определяют показатели экспоненты свободной составляющей. Корни могут иметь следующий вид:
определяют показатели экспоненты свободной составляющей. Корни могут иметь следующий вид:
1. 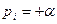 (действительный положительный корень).
(действительный положительный корень).
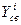
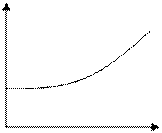
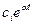 При положительном действительном корне система
При положительном действительном корне система
апериодически неустойчива. 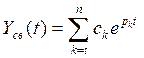
t
2. 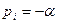 (отрицательный действительный корень)
(отрицательный действительный корень)
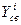

Соответствует устойчивому апериодическому процессу.
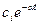
t
3. 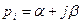 (комплексный корень с положительной действительной частью)
(комплексный корень с положительной действительной частью)
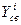
При комплексном корне с положительной действительной частью движение будет колебательное, неустойчивое.
t
4. 4.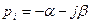 (комплексный корень с отрицательной действительной частью)
(комплексный корень с отрицательной действительной частью)
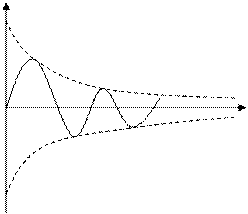
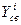
При таком корне движение колебательное, устойчивое.
t
5. 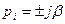
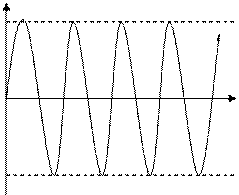
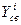
Система находится на границе устойчивости, движение имеет колебательный вид(граница колебательной устойчивости).
t
6. 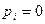
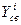
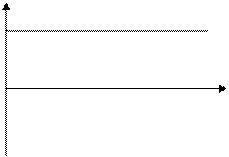
Система находится на границе апериодической устойчивости.
t
Для того чтобы САУ была устойчивой необходимо и достаточно, чтобы корни уравнения (3) были либо отрицательными, либо комплексными с отрицательной действительной частью. Уравнение (3) является характеристическим.
Передаточная функция:
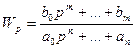
 2014-02-02
2014-02-02 1962
1962
