Имеется САУ:
 |
1. Замкнутая система.
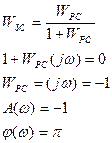
2. Разомкнутая система.
Разомкнутая система неустойчива и количество положительных корней характеристического уравнения разомкнутой системы равно m.
 Im
Im
-1 Re
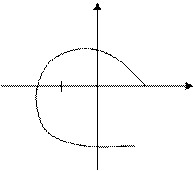
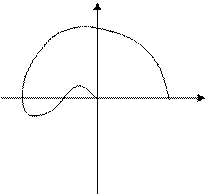
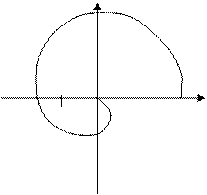
При анализе устойчивой системы, при неустойчивой разомкнутой системе будем считать положительным направлением годографа – против часовой стрелки. Отрицательным направлением годографа – почасовой стрелке, или снизу вверх при пересечении действительной оси. Тогда критерий Найквиста звучит так: если система неустойчива в разомкнутом состоянии и имеет m положительных корней характеристического уравнения, то система в замкнутом состоянии будет устойчива, если разность между количеством положительных переходов и количеством отрицательных переходов отрезка 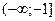 действительной оси будет равна m/2.
действительной оси будет равна m/2.
 Im Im
Im Im
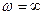 Re
Re 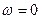
-1 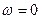
 Re
Re
 Im
Im
 Re
Re
-1 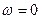
Система находится на границе устойчивости, если годограф, соответствующий амплитудно-фазовой характеристики разомкнутой системы хотя бы один раз пересечет точку (-1;0).
САУ будет устойчива, если годограф, соответствующей амплитудно-фазовой характеристики разомкнутой системы охватывает точку (-1;0) m/2 раз.
m=0
Im
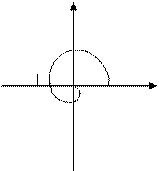 Re
-1
Re
-1
| m=2
Im
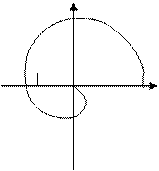 Re
-1
Re
-1
| m=3
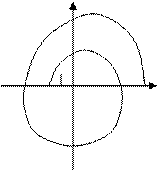
Пполупереход означает, что АФХ либо начинается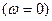 , либо заканчивается , либо заканчивается 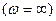 на действительном отрезке на действительном отрезке  Im
Im
-1 Re
Отрицательных переходов нет |
или
 Im
Re Im
Re
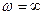 -1
-1 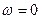
|
Пример.
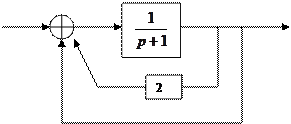
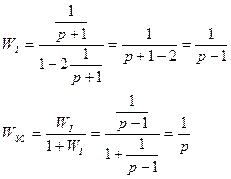
Для критерия Михайлова составляем характеристическое уравнение 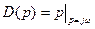
 Im
Im
 |
 Re
Re
В качестве анализа рассматривается АФХ разомкнутой системы:
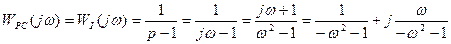
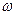
| Re | Im |
| -1 | ||
| -1/2 | -1/2 | |
| -1/101 | -1/101 | |
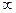
| -0 |
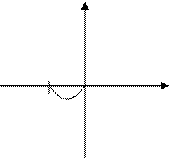 Im
Im
Re
-1
 2014-02-02
2014-02-02 604
604

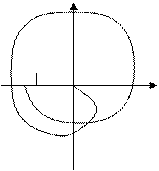
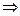 система устойчивая
система устойчивая






