В условиях действия схемы Бернулли (производится 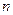 независимых испытаний, событие
независимых испытаний, событие  наступает ровно
наступает ровно  раз, вероятность наступления
раз, вероятность наступления  в одном испытании равна
в одном испытании равна 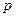 ) при большом
) при большом 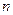 подсчитать
подсчитать  по формуле Бернулли затруднительно (нужно подсчитать большие факториалы, большие степени и т.п.).
по формуле Бернулли затруднительно (нужно подсчитать большие факториалы, большие степени и т.п.).
Для упрощения расчётов придумали формулу, но приближённую (пришлось «заплатить точностью»). Приведем без доказательства соответствующую теорему.
Локальная теорема Муавра-Лапласа. Если вероятность 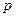 наступления события
наступления события  в каждом из
в каждом из 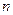 независимых испытаний постоянна,
независимых испытаний постоянна, 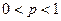 , число
, число 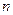 испытаний велико, то вероятность
испытаний велико, то вероятность  того, что в
того, что в 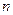 независимых испытаниях событие
независимых испытаниях событие  наступит ровно
наступит ровно  раз, приближённо равно:
раз, приближённо равно:
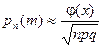 ,
,
где  ,
, 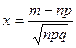 ,
, 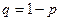 .
.
Функция 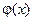 затабулирована (в [2] значения этой функции даются в таблице приложения 1).
затабулирована (в [2] значения этой функции даются в таблице приложения 1).
При использовании этой таблицы полезно иметь в виду, что: функция 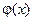 чётная (т.е.
чётная (т.е. 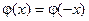 ); функция
); функция 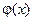 убывает при
убывает при 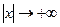 ; функция
; функция 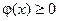 .
.
_______________
Пример. Найти вероятность того, что при 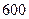 выстрелах мишень будет поражена ровно
выстрелах мишень будет поражена ровно 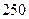 раз, если вероятность поражения мишени при одном выстреле равна
раз, если вероятность поражения мишени при одном выстреле равна 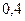 .
.
Решение. Понятно, что искомую вероятность  можно найти по формуле Бернулли, но кто возьмется подсчитать
можно найти по формуле Бернулли, но кто возьмется подсчитать  (т.е.
(т.е. 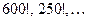 )? А с помощью локальной теоремы Муавра-Лапласа - запросто! Здесь
)? А с помощью локальной теоремы Муавра-Лапласа - запросто! Здесь 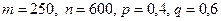 :
:
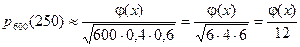 ,
,
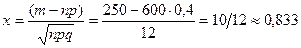 .
.
Поэтому по таблице приложения 1 находим 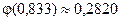 , откуда:
, откуда:
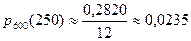 .
.
Теперь пусть перед нами поставлена следующая задача. Найти вероятность того, что из достаточно большого числа объектов от 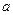 до
до 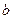 объектов имеют определённое свойство:
объектов имеют определённое свойство: 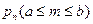 .
.
Например, нужно найти вероятность того, что из 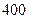 семей от
семей от 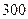 до
до 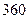 семей имеют автомобиль:
семей имеют автомобиль:
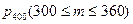 .
.
В условиях действия схемы Бернулли (производится 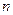 независимых испытаний, событие
независимых испытаний, событие  наступает ровно
наступает ровно  раз, вероятность наступления
раз, вероятность наступления  в одном испытании равна
в одном испытании равна 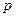 ) при большом
) при большом 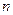 подсчитать
подсчитать 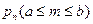 по формуле Бернулли затруднительно (нужно подсчитать большие факториалы, большие степени и т.п.). Подсчитать по локальной теореме Муавра-Лапласа? Но она приближённая, а поэтому мы сложим большое число ошибок и в итоге получим пшик!
по формуле Бернулли затруднительно (нужно подсчитать большие факториалы, большие степени и т.п.). Подсчитать по локальной теореме Муавра-Лапласа? Но она приближённая, а поэтому мы сложим большое число ошибок и в итоге получим пшик!
На помощь приходит интегральная теорема Муавра-Лапласа, которую также приведём без доказательства.
Интегральная теорема Муавра-Лапласа. Если вероятность 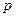 наступления события
наступления события  в каждом из
в каждом из 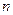 независимых испытаний постоянна,
независимых испытаний постоянна, 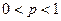 , то вероятность того, что число
, то вероятность того, что число  наступления события
наступления события  в
в 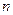 независимых испытаниях заключена в пределах от «
независимых испытаниях заключена в пределах от «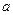 » до «
» до «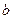 » (включительно) при достаточно большом числе
» (включительно) при достаточно большом числе 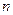 приближённо равна
приближённо равна
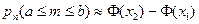 ,
,
где функция 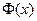 равна
равна 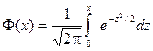 (функция Лапласа),
(функция Лапласа), 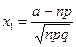 ,
, 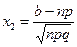 ,
, 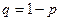 .
.
Функция 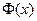 затабулирована (в [2] значения этой функции даются в таблице приложения 2).
затабулирована (в [2] значения этой функции даются в таблице приложения 2).
При использовании этой таблицы полезно иметь в виду, что: функция 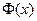 нечётная (
нечётная (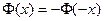 ); функция
); функция 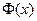 возрастает при увеличении положительного значения
возрастает при увеличении положительного значения 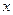 ; функция
; функция 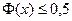 .
.
_______________
Пример. Вероятность появления события в каждом из 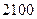 независимых испытаний равна
независимых испытаний равна 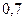 . Найти вероятность того, что событие появится не менее
. Найти вероятность того, что событие появится не менее 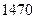 раз.
раз.
Решение. Нас интересует вероятность
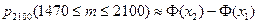 ,
,
где
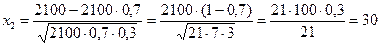 ,
,
следовательно, надо отыскать 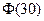 , но в табл. приложения 2 из [2] даётся только значение
, но в табл. приложения 2 из [2] даётся только значение 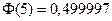 (для больших значений аргумента значений не приводится). Но так как
(для больших значений аргумента значений не приводится). Но так как 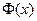 возрастает при значениях
возрастает при значениях 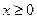 и
и 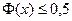 , то заключаем, что
, то заключаем, что 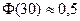 .
.
Кроме того 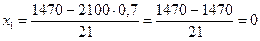 , поэтому
, поэтому 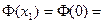
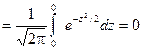 (по свойству определенного интеграла). Отсюда:
(по свойству определенного интеграла). Отсюда:
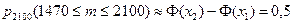 .
.
 2014-02-02
2014-02-02 644
644








