Постановка задачи численного дифференцирования

Численное дифференцирование функции.

В точках 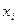, 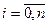-известны значения функции 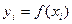. Задача численного дифференцирования – найти значение производной f’ или f” или … в любой наперед заданной точке х. Поступаем также как при интерполяции.

Общие идеи:

Заменяем неизвестную функцию f на интерполирующий многочлен Р.

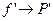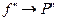; , а её производная И.М. Продифференцировав формулы для И.М. Схема Эйткена сразу отпадает, т.к. это схема, а не формула.

Формула Лагранжа громоздка, следовательно, будем дифференцировать формулу Ньютона И.М.