В магнитном поле

По перемещению проводника и контура с током

Теорема Гаусса для магнитного поля. Работа

Потоком вектора магнитной индукции через площадку dS называется скалярное произведение

dF = B×dS = B_n×dS. (3.37)

Здесь B_n = Bcosa – проекция вектора B на направление нормали к площадке dS. Если по контуру течёт ток, то положительное направление вектора нормали к поверхности связывают правилом правого винта с направлением тока в контуре. Таким образом, магнитный поток, создаваемый самим током контура, всегда положителен. Исходя из уравнения (3.37), полный поток через контур

F = ò B×dS = ò B_n×dS. (3.38)

Если поле однородно по плоской поверхности, то

F = B×S. (3.39)

Из последнего соотношения следует определение единицы измерения магнитного потока, которая называется вебер (Вб): 1 Вб – это магнитный поток через 1 м² плоской поверхности индукции магнитного поля в 1 Т при параллельном направлении индукции и вектора нормали к поверхности.

Для магнитного потока справедлива теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю

ò B×dS = ò B_n×dS =0. (3.40)

Аналогичная теорема для вектора напряжённости электрического поля звучит так: поток вектора напряжённости электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную

ò E d S = Sq_i/e_{0 .} (3.41)

Таким образом, теорема Гаусса для магнитного поля отражает факт отсутствия в природе магнитных зарядов, и что линии индукции магнитного поля суть замкнутые линии. В качестве примера рассмотрим, чему равен магнитный поток, создаваемый соленоидом, через соленоид. Поскольку внутри соленоида магнитное поле однородно по сечению соленоида и совпадает с направлением нормали к одному витку, то магнитный поток через один виток будет равен (см. формулу (3.11) для магнитного поля соленоида)

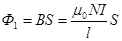. (3.42)

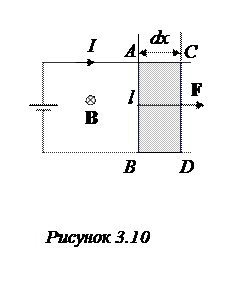Магнитный поток через весь соленоид будет очевидно равен магнитному потоку через 1 виток, умноженному на число витков, и эта величина называется потокосцеплением

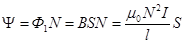. (3.43)

Если проводник длиной l с током I не закреплён (участок АБ на рис.3.10), то под действием силы Ампера он будет перемещаться в магнитном поле B в направлении x. По определению, элементарная работа будет равна

dA=Fdx=IBldx=IBdS=IdФ, (3.44)

где dФ – магнитный поток через поверхность dS, прочерчиваемую проводником при его движении. Таким образом, получили, что работа по перемещению проводника с током в магнитном поле равна произведению силы тока в проводнике на магнитный поток через поверхность, которую пересекает проводник при своём движении. Можно показать, что полученная формула справедлива и при произвольном направлении вектора В:

dA= IdФ. (3.45)

Выражение для работы по перемещению замкнутого контура оказывается подобным выражению (3.45) и для произвольного конечного перемещения контура в магнитном поле имеет вид

A = IDФ, (3.46)

т.е. равно произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.