Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.
1. Решение систем дифференциальных и интегральных уравнений — с помощью преобразования Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.
2. Расчёт передаточных функций динамических систем, таких, к примеру, как аналоговые фильтры.
3. Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов — так как выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, преобразование Лапласа позволяет заменить эту операцию на простое умножение.
4. Расчёт электрических схем. Производится путём решения дифференциальных уравнений, описывающих схему операторным методом.
5. Решение нестационарных задач математической физики.
Пусть дано линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами 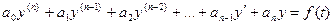 (5), где правая часть есть функция, зависящая от t.
(5), где правая часть есть функция, зависящая от t.
Требуется найти решение 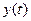 этого уравнения, удовлетворяющее начальным условиям
этого уравнения, удовлетворяющее начальным условиям 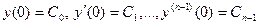 (6).
(6).
Для этого необходимо:
1. Применить к обеим частям уравнения преобразование Лапласа и, принимая во внимание свойства преобразования Лапласа (1, 5) и начальные условия составить операторное уравнение.
Замечание: для удобства операцию применения преобразования Лапласа к дифференциальному уравнению (5) условимся символически обозначать через L, т.е. 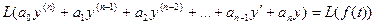 , что приведёт к соответствующему операторному уравнению.
, что приведёт к соответствующему операторному уравнению.
2. Решить операторное уравнение и найти операторное решение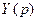 .
.
3. По найденному решению найти соответствующий этому решению оригинал 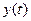 , который и будет решением уравнения, удовлетворяющим начальным условиям.
, который и будет решением уравнения, удовлетворяющим начальным условиям.
Пример: Решить уравнение 
Решение: 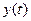 - искомое решение
- искомое решение
Применяем преобразование Лапласа к обеим частям уравнения, используя свойства 1, 5 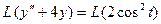
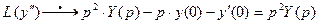
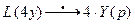

>> syms t p
>> f=laplace(cos(t)^2,t,p)
f = (2+p^2)/(p^2+4)/p
Составляем операторное уравнение: 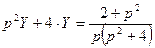
>> syms Y p
>> Y=solve('p^2*Y+4*Y=(2+p^2)/(p^2+4)/p','Y')
Y = (2+p^2)/(p^2+4)^2/p % получили операторное решение уравнения
% Находим искомое решение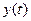
>> y=ilaplace(Y,t)
y = -1/8*cos(2*t)+1/8*t*sin(2*t)+1/8
Ответ: 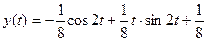
Проверка с помощью функции dsolve
>> y=dsolve('D2y+4*y=cos(t)^2','Dy(0)=0','y(0)=0')
y = -1/8*cos(2*t)+1/8*t*sin(2*t)+1/8
 2014-02-02
2014-02-02 4724
4724
