1. Заменяем каждое дифференциальное уравнение системы соответствующим операторным уравнением и получаем систему линейных алгебраических уравнений относительно изображений искомых функций.
2. Решив алгебраическую систему, получаем операторное решение системы дифференциальных уравнений.
3. Восстановив по операторному решению оригинал, имеем искомое частное решение.
Пример: Решить систему уравнений 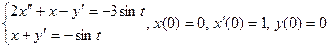
Решение: 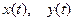 - частные решения.
- частные решения.

Используя преобразование Лапласа получаем:
>> laplace(sin(t),p)
ans = 1/(p^2+1)
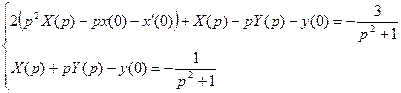
Подставляем начальные условия. Получаем систему операторных уравнений
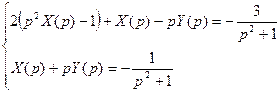
>> syms X Y p
[X Y]=solve('2*(p^2*X-1)+X-p*Y=-3/(p^2+1)','X+p*Y=-1/(p^2+1)','X','Y')
X =(p^2-1)/(p^4+2*p^2+1)
Y =-2*p/(p^4+2*p^2+1)
>> y=ilaplace(Y,t)
y =-t*sin(t)
>> x=ilaplace(X,t)
x =t*cos(t)
Ответ: 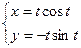
 2014-02-02
2014-02-02 843
843







