2014-02-02
736
1. Линейность. Пусть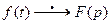 
, 
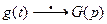и λ, μ – произвольные комплексные числа. Тогда 
.
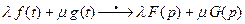Пример: найти изображение соответствующее оригиналу
>> syms t p
>> laplace(6*t^2,p)+laplace(4*cos(t),p)-laplace(5*sin(t),p)
ans =12/p^3+4*p/(p^2+1)-5/(p^2+1)
ИЛИ
>> laplace(6*t^2+4*cos(t)-5*sin(t),p)
ans =(12*p^2+12+4*p^4-5*p^3)/p^3/(p^2+1)
2. Теорема подобия. Если f (t) – функция-оригинал и 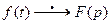, то для любого λ > 0 справедливо соотношение 
.
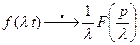Пример: найти изображение, соответствующее оригиналу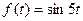 
Решение: 
3. Теорема смещения. Если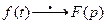 
, то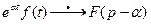 
. Здесь α – произвольное комплексное число. Умножение оригинала на функцию 
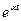приводит к смещению на величину α аргумента изображения.
Пример: найти изображение, соответствующее оригиналу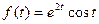 
Решение: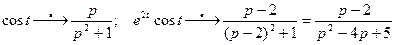 
>> laplace(cos(t),p)
ans = p/(p^2+1)
>> laplace(exp(2*t)*cos(t),p)
ans =(p-2)/(p^2-4*p+5)
4. Теорема запаздывания. Если 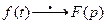, то для любого τ > 0 имеет место соотношение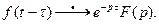 
Пример: найти изображение, соответствующее оригиналу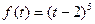 
Решение: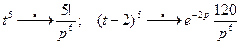 
>> syms t p
>> laplace((t-2)^5,p)
ans = -8*(-15+30*p-30*p^2+20*p^3-10*p^4+4*p^5)/p^6 % ML раскрывает скобки и для каждого слагаемого ищет изображение
5. Теорема дифференцирования оригинала. Если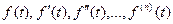 
являются оригиналами и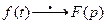, то 
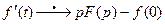и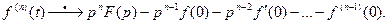 
.
6. Теорема интегрирования оригинала. Если f (t) – функция-оригинал и 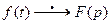, то
, интегрированию оригинала соответствует деление изображения на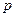 
.
Пример: Найти изображение интеграла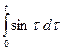
Решение: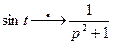 
. Тогда 
>> syms h
>> syms h;int(sin(h),0,t)
ans =1-cos(t)
>> laplace(sin(t),p)
ans =1/(p^2+1)
7. Теорема дифференцирования изображения. Если f (t) – функция-оригинал и 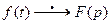, то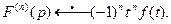 
Таким образом, дифференцирование изображения влечёт за собой умножение оригинала на 
.
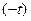Пример: найти изображение функции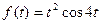 
, используя свойства преобразования Лапласа. Результат проверить, используя встроенную функцию.
>> syms t p
>> f=laplace(cos(4*t),t,p)
f =p/(p^2+16)
>> diff(f,p,2) % по свойству 7 дифференцируем 2 раза изображение.
ans =-6/(p^2+16)^2*p+8*p^3/(p^2+16)^3
>> simplify(ans)
ans =2*p*(p^2-48)/(p^2+16)^3
проверка
>> laplace(t^2*cos(4*t),t,p)
ans =2*p*(p^2-48)/(p^2+16)^3
8. Теорема интегрирования изображения. Если функция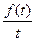 
является оригиналом, то из 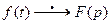следует 
.
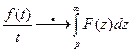9. Теорема умножения изображений (теорема Бореля). Произведение двух изображений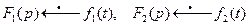 
также является изображением, причём 
.
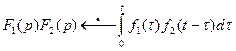Интеграл в правой части называется свёрткой функций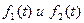 
обозначается символом 
.
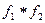Пример: найти оригинал, соответствующий изображению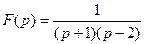 
.
Решение: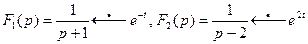 
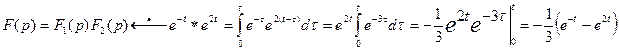
>> F=1/((p-2)*(p+1));
>> ilaplace(F,t)
ans =1/3*exp(2*t)-1/3*exp(-t)
Пример: получить оригинал функции 
>> syms a b p t L
>> L=(a+b*p)/p^2;
>> iLaplace(L,t)
ans =a*t+b
