Пример 5. Раисе определялось, что каждый из пяти лазерных компьютерных принтером в департаменте энергетики (DOE) требует ремонта после примерно 20 часов работы

Раисе определялось, что каждый из пяти лазерных компьютерных принтером в департаменте энергетики (DOE) требует ремонта после примерно 20 часов работы. Поломки определяю] с» распределением Пуассона. Один техник может отремонтировать принтер м среднем за два часа и соответствии с экспоненциаль­ным распределением. Поломка принтера обходится и $ 120 / 4, техникам платят $ 25 / 4. Должен ли департамент энергетики принять второго техника?

Предположим, второй техник может чинить принтер в среднем за два часа. Считаем, что ограниченный источник равен пяти принтерам, чтобы сравнить затраты одного или двух техников:

1) отмечаем, что Т = 2 ч и U = 20 ч;

2) тогда 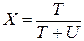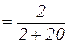= 2 / 22 =.091 (округляем до.090);

Этот анализ показал, что, имея только одного техника на дежурстве, мы получим малую экономию в размере нескольких долларов в час ($ 105.20 – 101.80 = $ 3.40).

Заключительная таблица очередей для n = 5

Продолжение заключительной таблицы очередей для n = 5

Продолжение заключительной таблицы очередей для n = 5

Многие практические проблемы теории очередей, которые встречаются в производственных и операционных сервисных сис­темах, имеют характеристики такие, как в четырех математиче­ских моделях, описанных ранее. Часто тем не менее в анализе проявляются вариации этих специфических случаев. Время обслуживания в мастерской ремонта автомобилей, например, следует тенденции нормального закона распределения вероятности, а не экспоненциального. Система регистрации колледжа, при которой одни студенты-старшекурсники имеют приоритет в выборе курсов и часов занятий по отношению ко всем другим студентам, может пользоваться примитивным приоритетом, определяющим дис­циплину очереди (такую, как FIFO). Система медицинского отбо­ра в армию – пример многофазной системы, более сложной, чем однофазная модель, обсуждаемая в этой главе. Новобранцу изме­ряют давление на одном аппарате, проверяют зрение на другом, снимают психиатрические показания на третьем и осматривают на четвертом. На каждой фазе новобранец должен занять другую очередь и ожидать в ней.

Модели применительно к этим случаям развивают операцион­ные исследования. Вычисления на основе математических формул носят более комплексный характер по сравнению с теми, которые рассматривались в этой главе. Многие реальные приложения очередей являются комплексом аналитических моделей. Ряд про­блем математически не описывается. Там, где это возможно, аналитически обычно используют имитационное компьютерное моделирование.